Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

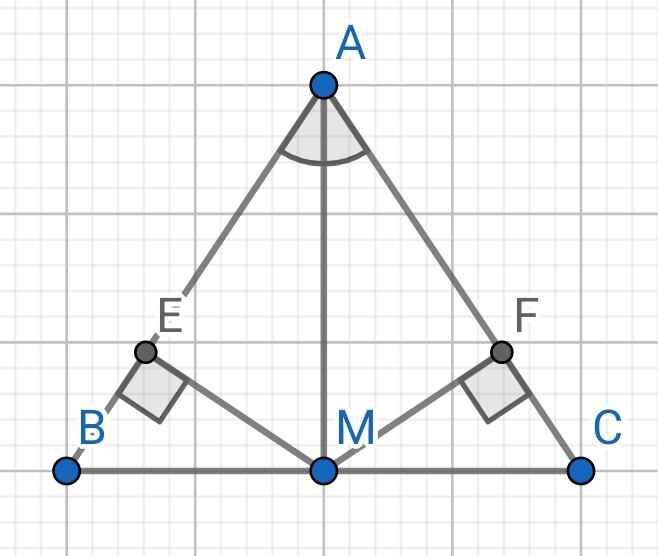 a) Do AM là tia phân giác của ∠BAC (gt)
a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AB = AC (gt)
∠BAM = ∠CAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ACM (c-g-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∠BAM = ∠CAM (cmt)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AME và ∆AMF có:
AM là cạnh chung
∠EAM = ∠FAM (cmt)
⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)
a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)
b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)
c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)

Cho △ABC có AB = AC, AM là phân giác của ∠BAC (M ∈ BC):
a, Chứng minh △ABM = △ACM.
b, Chứng minh M là trung điểm của BC và AM ⊥ BC.
c, Kẻ MF ⊥ AB (F ∈ AB) và ME ⊥ AC (E ∈ AC). Chứng minh EF // BC.
Giải:
a,
- Xét 2 △ABM và △ACM, có:
AB = AC (theo giả thiết)
∠CAM = ∠BAM (AM là phân giác của ∠BAC)
AM_cạnh chung
=> △ABM = △ACM (c.g.c)
b,
- Có △ABM = △ACM (chứng minh trên)
=> MC = MB (2 cạnh tương ứng)
=> M là trung điểm của BC
=> ∠AMC = ∠AMB (2 góc tương ứng)
mà 2 ∠AMC và ∠AMB kề bù
=> ∠AMC = ∠AMB = \(\dfrac{180^o}{2}\) = 90o
<=> AM ⊥ BC
c,
- Xét 2 △AEM và △AFM, có:
∠AEM = ∠AFM = 90o
AM_cạnh chung
∠EAM = ∠FAM (AM là phân giác của ∠EAF)
=> △AEM = △AFM (cạnh huyền - góc nhọn)
=> AE = AF (2 cạnh tương ứng)
<=> △AEF cân tại A
=> ∠AEF = \(\dfrac{180^o-\text{∠}EAF}{2}\) (số đo của một góc ở đáy trong △AEF cân tại A) (1)
Có △ABC cân tại A (AB = AC)
=> ∠ACB = \(\dfrac{180^o-\text{∠}BAC}{2}\) (số đo của một góc ở đáy trong ΔABC cân tại A) (2)
Từ (1) và (2) suy ra ∠AEF = ∠ACB
mà ∠AEF và ∠ACB ở vị trí đồng vị
=> EF//BC

a) Xét ΔABM và ΔACM có
AB=AC(gt)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)
b) Ta có: ΔABM=ΔACM(cmt)
nên \(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
hay \(\widehat{EAM}=\widehat{FAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)(cmt)
Do đó: ΔAEM=ΔAFM(cạnh huyền-góc nhọn)
⇒AE=AF(hai cạnh tương ứng)
c) Xét ΔABC có AB=AC(gt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
⇒\(\widehat{B}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(1)
Xét ΔAEF có AE=AF(cmt)
nên ΔAEF cân tại A(Định nghĩa tam giác cân)
⇒\(\widehat{AEF}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAEF cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{B}=\widehat{AEF}\)
mà \(\widehat{B}\) và \(\widehat{AEF}\) là hai góc ở vị trí đồng vị
nên EF//BC(Dấu hiệu nhận biết hai đường thẳng song song)
có gì đó sai sai ở đây từ M mà kẻ AE vuông góc với AB là sao

AB = AC => Tam giác ABC cân tại A
a. Xét tam giác AMB và tam giác AMC
AB = AC ( gt )
Góc B = góc C ( ABC cân )
BM = CM ( gt )
Vậy...... ( c.g.c)
=> góc BAM = góc CAM ( 2 góc tương ứng )
=> AM là phân giác góc A
b. trong tam giác cân ABC đường phân giác cũng là đường cao
=> AM vuông BC
c.tam giác MEF là tam giác cân vì:
xét tam giác vuông BME và tam giác vuông CMF
Góc B = góc C
MB = MC ( gt )
Vậy....( cạnh huyền. góc nhọn )
=> ME = MF ( 2 cạnh tương ứng )
Chúc bạn học tốt !!!
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M

a)Xét tgiac ABM và tgiac ACM,ta cí:
AB=AC(vì tgiac ABC cân tại A)
MC=MB(giả thiết)
AM là cạnh chung
=>tgiac ABM = tgiac ACM(c.c.c)

a) Xét tam giác ABM va tam giác ACM
Ta có: AB=AC(gt)
Góc B= góc C(gt)
MB=MC(Vì M là trung điểm của BC)
Vậy tam giác ABM=tam giác ACM(c.g.c)
b) Xét tam giác EBM và tam giác ECM
Ta có: góc BEM = góc CFM=90 độ
góc B =góc C(gt)
BM=CM(gt)
Vậy tam giác EBM= tam giác ECM(ch-gn )
=>BE=CE (2 cạnh tương ứng)
Ta có AE=AB-EB
AF=AC-FC
Mà AB=AC
EB=FC(cmt)
=>AE=AF
Xét tam giác AEM và tam giác AFM
AE=AF(cmt)
góc AEM= góc AFM=900
AM:Cạnh chung
Vây tam giác AEM= tam giác AFM(ch-cgv)
c) Gọi {T}=AM giao nhau với EF
Xét tam giác AET và tam giác AFT
AE=AF(cmt)
góc EAT= góc AFT( vì tam giác AEM=tam giác AFM)
AT: cạnh chung
Vậy tam giác AET =tam giác AFT (c.g.c)
=>góc ATE = góc AFT(2 góc tương ứng)
mà góc ATE + góc AFT= 1800
=> GÓC ATE =GÓC AFT= 900
Vậy AM vuông góc với EF
NẾU ĐÚG THÌ CHO MÌNH NHA

a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
AB = AC (gt)
AM chung
BM = MC (M là trung điểm BC)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-c-c\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\) (hai góc tương ứng)
\(\Rightarrow AM\) là tia phân giác của \(\widehat{BAC}\)
b) Xét hai tam giác vuông \(\Delta AME\) và \(\Delta AMF\) có:
\(\widehat{AEM}=\widehat{AFM}=90^0\)
AM chung
\(\widehat{MAE}=\widehat{MAF}\) (do AM là tia phân giác của \(\widehat{BAC}\))
\(\Rightarrow\Delta AME=\Delta AMF\) (cạnh huyền - góc nhọn)
\(\Rightarrow AE=AF\) (hai cạnh tương ứng)

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔMBA vuông tại M và ΔMCD vuông tại M có
MB=MC
MA=MD
Do đó: ΔMBA=ΔMCD
=>\(\widehat{MBA}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
\(\widehat{MBE}=\widehat{MCF}\)
Do đó: ΔBEM=ΔCFM
=>ME=MF
ΔBEM=ΔCFM
=>\(\widehat{BME}=\widehat{CMF}\)
mà \(\widehat{BME}+\widehat{EMC}=180^0\)(hai góc kề bù)
nên \(\widehat{CMF}+\widehat{EMC}=180^0\)
=>F,M,E thẳng hàng
mà MF=ME
nên M là trung điểm của EF

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM