4)Cho tam giác ABC cân tại A. Vẽ AH ⊥ BC
a)Chứng minh: ∆AHB = ∆AHC ;
b)Vẽ HM ⊥ AB, HN ⊥ AC. Chứng minh ∆AMN cân
c)Chứng minh MN // BC ;
d)Chứng minh AH2 + BM2 = AN2 + BH2
5)Cho tam giác ABC vuông tại A, có AB < AC. Trên cạnh BC lấy điểm D sao cho BD = BA. Kẻ AH vuông góc với BC, kẻ DK vuông góc với AC
.a)Chứng minh : ADBDABˆˆ=;
b)Chứng minh : AD là phân giác của góc HAC
c) Chứng minh : AK = AH.
6)Cho tam giác cân ABC có AB = AC = 5 cm , BC = 8 cm . Kẻ AH vuông góc với BC (H ∈ BC)
a) Chứng minh : HB = HC và ·CAH = ·BAH
b)Tính độ dài AH ?
c)Kẻ HD vuông góc AB ( D ∈AB), kẻ HE vuông góc với AC(E ∈AC). Chứng minh : DE//BC
7)Cho tam giác ABC , có AC < AB , M là trung điểm BC, vẽ phân giác AD. Từ M vẽ đường thẳng vuông góc với AD tại H, đường thẳng này cắt tia AC tại F ,cắt AB tại E.
Chứng minh rằng :a) ∆ AFE cân
b) Vẽ đường thẳng Bx // EF, cắt AC tại K. Chứng minh rằng : KF = BE
c) Chứng minh rằng : AE = (AB+AC):2
8) Cho tam giác DEF vuông tại D, phân giác EB . Kẻ BI vuông góc với EF tại I . Gọi H là giao điểm của ED và IB .
Chứng minh : a) ΔEDB = Δ EIB ;
b) HB = BF
c) Gọi K là trung điểm của HF. Chứng minh 3 điểm E, B, K thẳng hàng ;
d) DI // HF
9) Cho tam giác ABC vuông tại A . Đường phân giác của góc B cắt AC tại H . Kẻ HE vuông góc với BC. Đường thẳng EH và BA cắt nhau tại I .
a)Chứng minh rẳng : ΔABH = ΔEBH ;
b)Chứng minh BH là trung trực của AE
c)Chứng minh BH vuông góc với IC . Có nhận xét gì về tam giác IBC
10) Cho ΔABC vuông tại A, M là trung điểm BC, vẽ MH ⊥AB. Trên tia đối tia MH lấy điểm K sao cho MK = MH.
a).CMR: ΔMHB = ΔMKC
b).CMR: AC = HK
c).CH cắt AM tại G, tia BG cắt AC tại I. CMR: I là trung điểm AC
11) Cho ∆ ABC cân tại A. Trên BC lấy D và E sao cho BD = CE ( D và E nằm ngoài tam giác ). Kẻ tia DI ⊥ AB,kẻ tia EK ⊥AC, DI cắt EK tại H.
a) CMR: ∆ ABE = ∆ ACD.
b) CMR: HD = HE.
c)Gọi O là giao điểm của CI và BK ;∆ OED là tam giác gì ? chứng minh.
d) CMR: AO là tia phân giác của góc BAC ?
e) A ,O , H thẳng hàng
12) Cho tam giác ABC cân ở A có AB = AC = 5 cm; kẻ AH ⊥ BC ( H ∈ BC)
a) Chứng minh BH = HC và BAH = CAH
b) Tính độ dài BH biết AH = 4 cm
c) Kẻ HD ⊥ AB ( d ∈ AB), kẻ EH ⊥ AC (E ∈ AC).
d) Tam giác ADE là tam giác gì? Vì sao?




Xét hai tam giác vuông ΔABH ΔABH và ΔACH ΔACH:
Ta có: AH cạnh chung
AB=AC
Vậy ΔABH ΔABH = ΔACH ΔACH (c.g.c)
AH là đường cao đồng thời đường trung tuyến của ΔABC ΔABC cân tại A (AB=AC)
Vậy HC= HB hay H là trung điểm BC
2. BH = HC = BC2= 122 = 6BC2 = 122 = 6 cm
Áp dụng định lí Py-ta-go:
AH = √AB2 − HB2= √102 − 62 = 8AH = AB2− HB2 = 102− 62 = 8 cm
3. Ta có: AK là đường cao ΔAEH ΔAEH
Mà KE = KH nên AK cũng là đường trung tuyến ΔAEH ΔAEH
Vậy ΔAEH ΔAEH cân tại A
Nên AE=AH (1)
4. Ta có: AI là đường cao ΔADH ΔADH
Mà IH = ID nên AI cũng là đường trung tuyến ΔADH ΔADH
Vậy ΔAEH ΔAEH cân tại A
Nên AD = AH (2)
Từ (1)(2) Suy ra: AE=AD hay ΔAED ΔAED cân tại A
5. Xét ΔAEF ΔAEF và ΔADF ΔADF:
Ta có: AF cạnh chung
AE=AD
\(\widehat{AEF}\)=\(\widehat{ADF}\) \(\widehat{AEF}\)=\(\widehat{ADF}\)
Vậy ΔAEFΔAEF =ΔADFΔADF (c.g.c)
Nên EF = FD; AF là đường trung tuyến ΔAED ΔAED cân nên đồng thời đường cao nên AF vuông góc ΔAED ΔAED (3)
AF vuông góc BC (4)
Từ (3)(4) Suy ra: DE//BC
6. Để A là trung điểm ED thì ΔABC ΔABC vuông cân tại A
Giả sử ΔABC ΔABC vuông cân tại A nên AH=HB (đường cao đồng thời trung tuyến) IA=IB (đường cao đồng thời trung tuyến)
Tứ giác ADBH có hai đường chéo cắt nhau tại trung điểm mổi đường nên ADBH là hình bình hành
CM tương tự cho tứ giác AECH
Mà C,H,B thẳng hàng và HC=HB nên E,A,D thẳng hàng và A là trung điểm ED
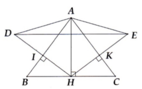
Hình đó nha bn ^^
#hoc_tot#
:>>>