Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

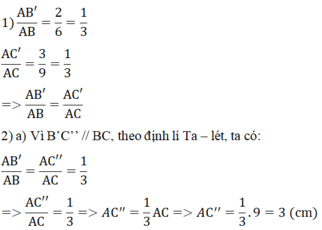
b) Trên đoạn thẳng AC ta có: AC’= AC’’= 3 cm nên
Khi đó, hai đường thẳng BC và B’C’ song song với nhau.

1: Xét ΔABC có DE//BC
nên AE/AC=AD/AB
=>AE/8=1/3
=>AE=8/3(cm)
2:
Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/10=1/3
=>DE=10/3(cm)
Xét tứ giác BDEF có
BD//EF
BF//DE
Do đó: BDEF là hình bình hành
=>BF=DE=10/3(cm)
3:
AD/AB=1/3
AE/AC=1/3
DE/BC=1/3
Do đó: AD/AB=AE/AC=DE/BC

Xét \(\Delta\)ABC có DE //BC
=> \(\frac{AD}{AB}=\frac{AE}{AC}\)( ta lét)
=> \(\frac{AC}{AB}=\frac{AE}{AD}=\frac{AC-EC}{AD}=\frac{AC-AD}{AD}\)( vì AD = CE)
=> \(\frac{AC}{AB}=\frac{AC}{AD}-1\)
Khi đó: \(\frac{10}{6}=\frac{10}{AD}-1\)
<=> \(\frac{10}{AD}=\frac{16}{6}\)
<=> AD= 10.6 : 16 = 3,75

Lời giải :
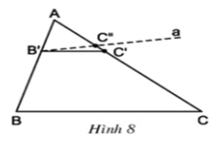
A B C B' C' a C''
Ta có : \(\frac{AB'}{AB}=\frac{AC'}{AC}\)( GT ) ( 1 )
+) Đường thẳng a đi qua B' song song với BC ( GT )
\(B'C''//BC\)( vì đường thẳng a cắt AC tại C'' )
\(\Rightarrow\frac{AB'}{AB}=\frac{AC''}{AC}\)( Định lí Ta lét ) ( 2 )
Từ ( 1 ) và ( 2 )
\(\Rightarrow AC'=AC''\)

a) +)Xét tg ABD có: CE //BD(gt)
Áp dụng đl Ta-let, ta có:
AB/AC=AD/AE
+) Xét tam giác ADC có: FE // CD(gt)
Áp dụng đl Ta-let,ta có:
AC/AF=AD/AE
b)Từ câu a), ta có:
AB/AC=AC/AF
->AC.AC=AB.AF
->AC^2=AB.AF

Tự vẽ hình.
a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
Từ (2), (3) và (4) => MODC=NODC⇒MO=NOMODC=NODC⇒MO=NO ( ĐPCM )

a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).
Vậy \(AC' = \frac{{16}}{3}cm\).
b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:
\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).
Vậy \(BD = \frac{{10}}{3}cm\).
Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)
Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))
Xét tứ giác \(B'C'DB\) có
\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)
c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
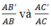
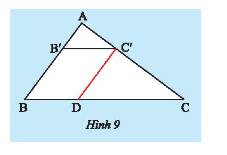
a) Ta có:
\(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3}\) và \(\frac{{AC'}}{{AC}} = \frac{5}{{15}} = \frac{1}{3}\).
b) Vì \(B'E//BC\) và\(B'E\) cắt \(AC\) tại \(E\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AE}}{{15}} \Rightarrow AE = \frac{{2.15}}{6} = 5cm\)
c) Ta có: \(AE = AC' = 5cm\).
d) Điểm \(E \equiv C'\) và đường thẳng \(B'C' \equiv B'E\).