Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: B
Ta có A(-1;3), B(1;0) và C(2;-1)
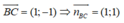
Phương trình đường thẳng BC có dạng: (x - 1) + (y - 0) = 0 ⇔ x + y - 1 = 0
Độ dài đường cao của tam giác ABC kẻ từ điểm C chính bằng khoảng cách từ điểm A đến đường thẳng BC:
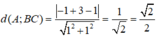
Câu 1: Diện tích tam giác là: \(\frac{h_A.a}{2}=\frac{3.6}{2}=9\)(đvdt)
Câu 2: Diện tích tam giác là: \(\frac{1}{2}ab.\sin C=\frac{1}{2}.4.5.\sin60^o=5\sqrt{3}\)(đvdt)
Câu 2: Ta có: \(\hept{\begin{cases}c^2=a^2+b^2-2ab.\cos C\\a^2+b^2>c^2\end{cases}\Rightarrow c^2>c^2-2ab.\cos C\Leftrightarrow2ab.\cos C>0}\)
\(\Rightarrow\cos C>0\Rightarrow C< 90^o\)
Vậy C là góc nhọn
a) Từ giả thiết suy ra \(\overrightarrow{AB}=\left(-6;8\right),\overrightarrow{AC}=\left(-4;3\right)\) do đó AB=10 và AC=5.
Gọi D là chân đường phân giác kẻ từ A
khi đó \(\overrightarrow{DB}=-2\overrightarrow{DC}\) suy ra \(D\left(-\frac{5}{3};-\frac{1}{3}\right)\)
Vậy độ dài đường phân giác trong kẻ từ A bằng \(AD=\sqrt{\left(3+\frac{5}{3}\right)^2+\left(-5+\frac{1}{3}\right)^2}=\frac{14\sqrt{2}}{3}\)
b) Gọi E là chân phân giác ngoài kẻ từ A
Khi đó \(\overrightarrow{EB}=2\overrightarrow{EC}\) suy ra E(1;-7)
Vậy nếu J là trung điểm DE thì \(J\left(-\frac{1}{3};-\frac{11}{3}\right)\)
a: Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{A}=180^0-75^0-45^0=60^0\)
Xét ΔABC có
\(\dfrac{AB}{sinC}=\dfrac{BC}{sinA}\)
=>\(\dfrac{AB}{sin45}=\dfrac{50}{sin60}\)
=>\(AB\simeq40,82\)
b: \(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC=\dfrac{1}{2}\cdot40,82\cdot50\cdot sin75\simeq985,73\)
c: Độ dài đường cao xuất phát từ A là:
\(2\cdot\dfrac{985.73}{50}=39,4292\left(\right)\)
a) Ta có: \(\overrightarrow {{u_{BC}}} = \overrightarrow {BC} = \left( { - 5; - 3} \right) \Rightarrow \overrightarrow {{n_{BC}}} = \left( {3; - 5} \right)\) . Vậy phương trình tổng quát của đường thẳng BC là: \(3\left( {x - 3} \right) - 5\left( {y - 2} \right) = 0 \Leftrightarrow 3x - 5y + 1 = 0\).
Độ dài đường cao AK của tam giác \(ABC\) hạ từ đỉnh A là: \(AK = d\left( {A,BC} \right) = \frac{{\left| {3.1 - 0.5 + 1} \right|}}{{\sqrt {{3^2} + {{\left( { - 5} \right)}^2}} }} = \frac{4}{{\sqrt {34} }}\)
b) Ta có: \(\overrightarrow {BC} = \left( { - 5; - 3} \right) \Rightarrow BC = \sqrt {{{\left( { - 5} \right)}^2} + {{\left( { - 3} \right)}^2}} = \sqrt {34} \)
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AK.BC = \frac{1}{2}.\frac{4}{{\sqrt {34} }}.\sqrt {34} = 2\)
Chọn A.
Hệ thức trung tuyến xuất phát từ đỉnh A của tam giác:
Mà b2 + c2 = 2a2 nên 
nên 
.
a) \(\cos A=-\dfrac{3}{5}\Rightarrow\widehat{A}\approx126^052'\)
b) \(AB:2x+y-1=0;AC=2x-y-3=0\)
c) Phân giác trong \(AD\) có phương trình : \(y+1=0\)
Đáp án: A
Ta có: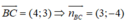
Đường thẳng BC đi qua B và có vecto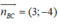
là vecto pháp tuyến:
BC: 3(x + 1) - 4(y - 0) = 0 ⇔ 3x - 4y + 3 = 0
Gọi AH là đường cao của tam giác ABC