Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy b = c.
Thêm đk của đề bài là \(\widehat{A}\leq 90^o\), vì nếu ngược lại thì \(a^2>2b^2\) và khi đó điều cần cm sẽ sai.
Do tam giác ABC cân tại A nên DE // BC.
Theo định lý Thales ta có: \(\dfrac{DE}{BC}=\dfrac{AE}{AB}\Leftrightarrow\dfrac{DE}{a}=\dfrac{AE}{b}\Leftrightarrow DE=\dfrac{a.AE}{b}\).
Ta lại có: \(\left\{{}\begin{matrix}AE^2-BE^2=AC^2-BC^2=b^2-a^2\\AE+BE=AB=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AE-BE=\dfrac{b^2-a^2}{b}\\AE+BE=b\end{matrix}\right.\Rightarrow AE=\left(\dfrac{b^2-a^2}{b}+b\right):2=\dfrac{2b^2-a^2}{2b}\).
Do đó \(DE=\dfrac{a\left(2b^2-a^2\right)}{2b^2}\).

a: Xét ΔCAB có CA^2+CB^2=AB^2
nên ΔCAB vuông tại C
Xét ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*25=15*20=300
=>CH=12(cm)
b: góc BCD+góc ACD=90 độ
góc BDC+góc HCD=90 độ
mà góc ACD=góc HCD
nên góc BCD=góc BDC
=>ΔBDC cân tại B
c: BC^2+BD^2+CD^2
=BC^2+BC^2+CD^2
=2BC^2+CD^2
=2(BH^2+HC^2)+CH^2+HD^2
=2BH^2+3CH^2+DH^2

trong tam giac vuong ABH Cco \(AH^2+BH^2=AB^2\Rightarrow AH^2=AB^2-BH^2\left(1\right)\)
AHC co \(AH^2+HC^2=AC^2\Rightarrow AH^2=AC^2-HC^2\left(2\right)\)
tu (1) va(2 ) suy ra \(AB^2-BH^2=AC^2-HC^2\Rightarrow AB^2+HC^2=AC^2+BH^2\)

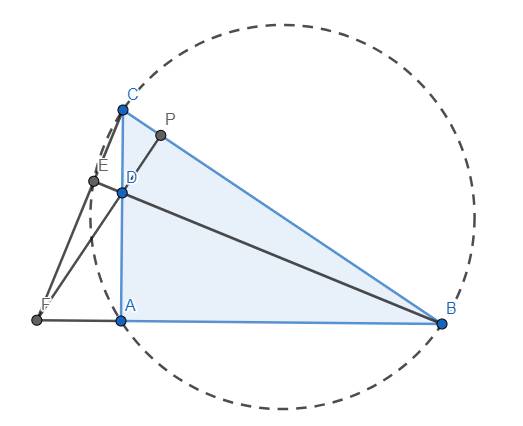
a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.
b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)
CMTT, ta có \(BD.BE=BC.BP\)
Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.

A B C H D K
a)) Xét tam giác ABC cân tại A có AH là đường cao => AH cũng là đường trung tuyến
=> BH = HC
Xét tam giác BCD có: AH // BD (vì cùng vuông góc với BC) và H là trung điểm của BC
=> AH là đường trung bình ==> \(AH=\frac{1}{2}BD\)=> BD = 2AH
b) Xét tam giác BCD vuông tịa B có BK là đường cao
=> \(\frac{1}{BK^2}=\frac{1}{BC^2}+\frac{1}{BD^2}\) (hệ thức lượng trong tam giác vuông)
=> \(\frac{1}{BK^2}=\frac{1}{BC^2}+\frac{1}{\left(2AH\right)^2}=\frac{1}{BC^2}+\frac{1}{4AH^2}\)

Lấy E sao cho A là trung điểm của CE
Xét ΔEBC có
BA là đường trung tuyến
BA=CE/2
Do đó: ΔEBC vuông tại E
Xét ΔCBE có AH//BE
nên AH/BE=CH/CB=1/2
=>AH=1/2BE
Xét ΔBEC vuông tại B có BK là đường cao
nên \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BE^2}\)
=>\(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)