Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì O là điểm cách đều 3 đỉnh của tam giác => O là giao điểm của 3 đường trung trực của tam giác ABC.
Vì tam giác ABC có AB=AC nên Tam giác ABC cân tại A => Đoạn AO thuộc đường trung trực, đường trung tuyến, đường phân giác của tam giác ABC => góc BAO = góc CAO (1)
Vì O cách đều 3 đỉnh của tam giác ABC nên ta có : OA = OB => tam giác AOB cân tại O
=>góc ABO = góc BAO (2)
từ (1) và (2) suy ra : góc ABO = góc CAO
b, Xét tam giác OMB và tam giác ONA có :
OA = OB ( cmt )
góc ABO = góc CAO hay góc MBO = góc NAO
BM = AN ( Gt )
=> tam giác OMB = tam giác ONA (c.g.c)
=> OM = ON hay O cách đều M và N

A B C M N O H K
a.Ta có điểm O cách đều 3 đỉnh tam giac => O là giao của 3 đường trung trực
Vì tgiac ABC có AB=AC=> tgiac ABC cân tại A mà AK vuông góc với BC => AK là tia phân giác của góc BAC
=> góc BAK= góc CAK(1)
Xét tgiac AHO và tgiac BHO có:
OH chung
góc AHO= góc BHO=90
HA=HB( vì OH là đường trung trực của AB)
=> tgiac AHO=tgiac BHO(c.g.c)
=> góc HBO= góc HAO(2 góc tương ứng)(2)
Từ (1) và(2) => góc ABO= góc CAO
b.xét tgiac MOB và tgiac NAO có:
BM=AN(gt)
góc MBO= góc NAO(cmt)
OB=OA(tính chất đường trung trực)
=> tgiac MOB=tgiac NAO(c.g.c)
=> Om=ON(2 cạnh tương ứng)
chị ơi giúp em bài nì với ạ
Ở miền trong góc tù xOy, vẽ các tia Oz, Ot sao cho Oz vuông góc với Ox, Ot vuông góc với Oy
a/ Góc toz là góc gì?
b/ So sánh góc xOt và yoz
c/ Tính tổng 2 góc xoy và tOz
vẽ giúp em cái hình được ko ạ

A B C o M N
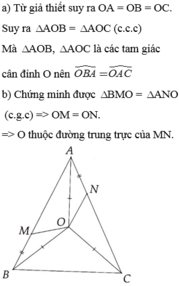
a) Xét tam giác BOA và tam giác AOC có:
OB=OA
OC=OA
AB=AC
=> \(\Delta BOA=\Delta AOC\)
=> góc OBA=góc OAC
b) Xét tam giác AON và tam giác BOM
có: AB=AO
BM=AN
\(\widehat{MBO}=\widehat{NAO}\)( theo a)
=> \(\Delta AON=\Delta BOM\)
=> OM=ON
=> O thuộc đường rung trực MN

a: Xét ΔPBC và ΔQCB có
PB=QC
\(\widehat{PBC}=\widehat{QCB}\)
BC chung
Do đo: ΔPBC=ΔQCB
Suy ra: \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
b: OB=OC
AB=AC
Do đó: AO là đường trung trực của BC
Ta có: ΔABC cân tại A
mà AO là đường trung trực
nên AO là đường phân giác
hay O cách đều hai cạnh AB và AC