Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC có
AB = AC ( = 5 cm )
=> tam giác ABC cân tại A ( ĐN)
Ta có AM là trung tuyến (gt)
=> AM là đg cao (t/c tam giác cân)
=> AM vuông BC (ĐN)
Ta có M là trung điểm của BC(AM là trung tuyến)
=> BM=CM=1/2 BC=6/2=3cm
Xét tam giác ABM có
AM vuông BC (cmt)
=> tam giác ABM vuông tại M (ĐN)
=> AM2 +BM2 = AB2 (đ/l Pitago)
Thay số: AM2 + 3 = 5
=> AM2= 5-3
=> AM2= 2
=> AM = \(\sqrt{2}\)(cm)
b) tam giác \(ABM\ne DCM\)
c) tam giác ACD ko cân

Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng

a, áp dụng định lí py-ta-go ta có:
BC2 =AB2+AC2
=> AC2=BC2−AB2
=> AC2=100−36
=> AC2=64 => AC=8 cm
vậy AC=8 cm
vì BC>AC>AB(10cm>8cm>6cm)
=>\(\widehat{A}\) > \(\widehat{B}\)>\(\widehat{C}\) (góc đối diện vs cạnh lớn hơn là góc lớn hơn) đpcm
b, Xét 2 t.giác vuông BCA và DCA có:
AB=AD(gt)
AC cạnh chung
=> ΔBCA=ΔDCA(cạnh huyền -cạnh góc vuông)
=> BC=DC(2 cạnh tương ứng)
=>\(\Delta\)BCD cân tại C (đpcm)

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

a, áp dụng tổng 3 góc trong 1 tam giác => góc AB= 25 độ
AC < AB ( 65 độ > 25 độ)
b, Xét tam giác BHC và tam giác BHE có: BH- chung ; BHA = BHE (=90 độ) ; AH = HE ( theo đề bài)
=> hai tam giác bằng nhau (c.g.c) => BA = BE => tam giác BEA cân tại B (đpcm)
c, Dễ dàng chứng minh được tam giác BEC = tam giác BAC
=> BEC = BAC = 90 độ
=> tam giác BEC vuông tại E (đpcm)
d, Ta có: MH đi qua trung điểm của AD và AE trong tam giác ADE => NM là đường trung bình của tam giác này => MN // DE (đpcm)
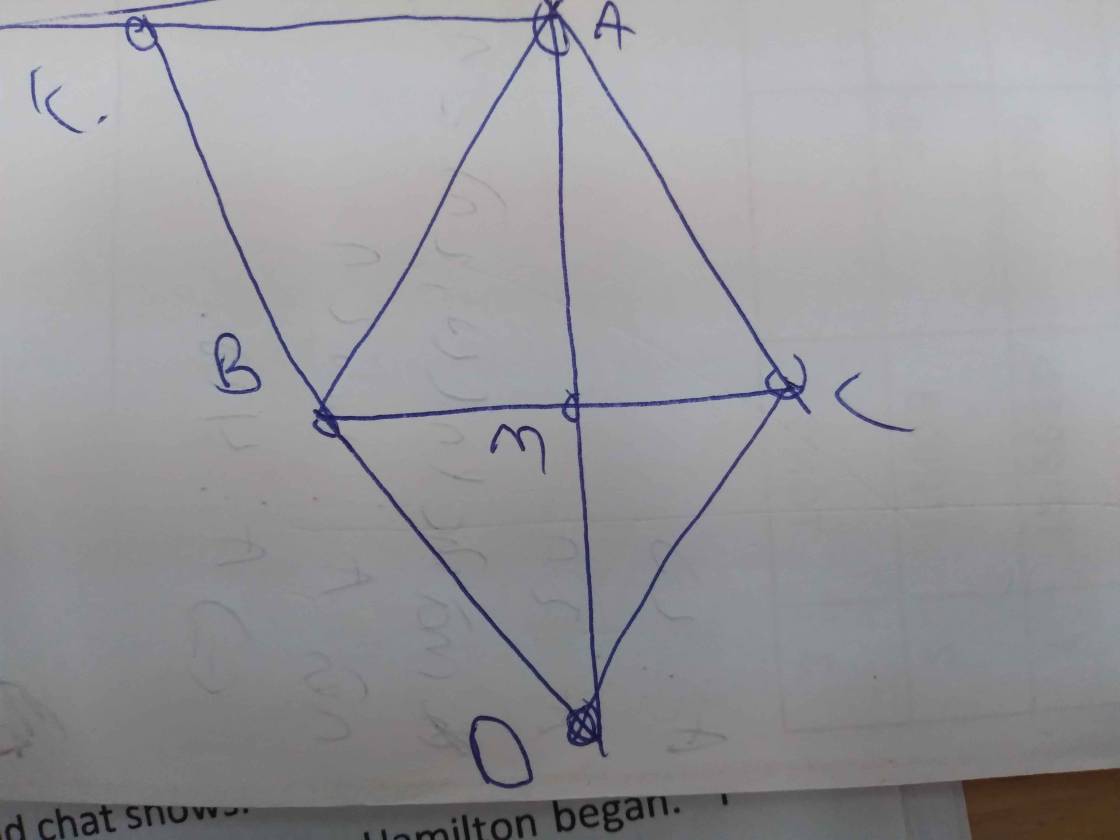
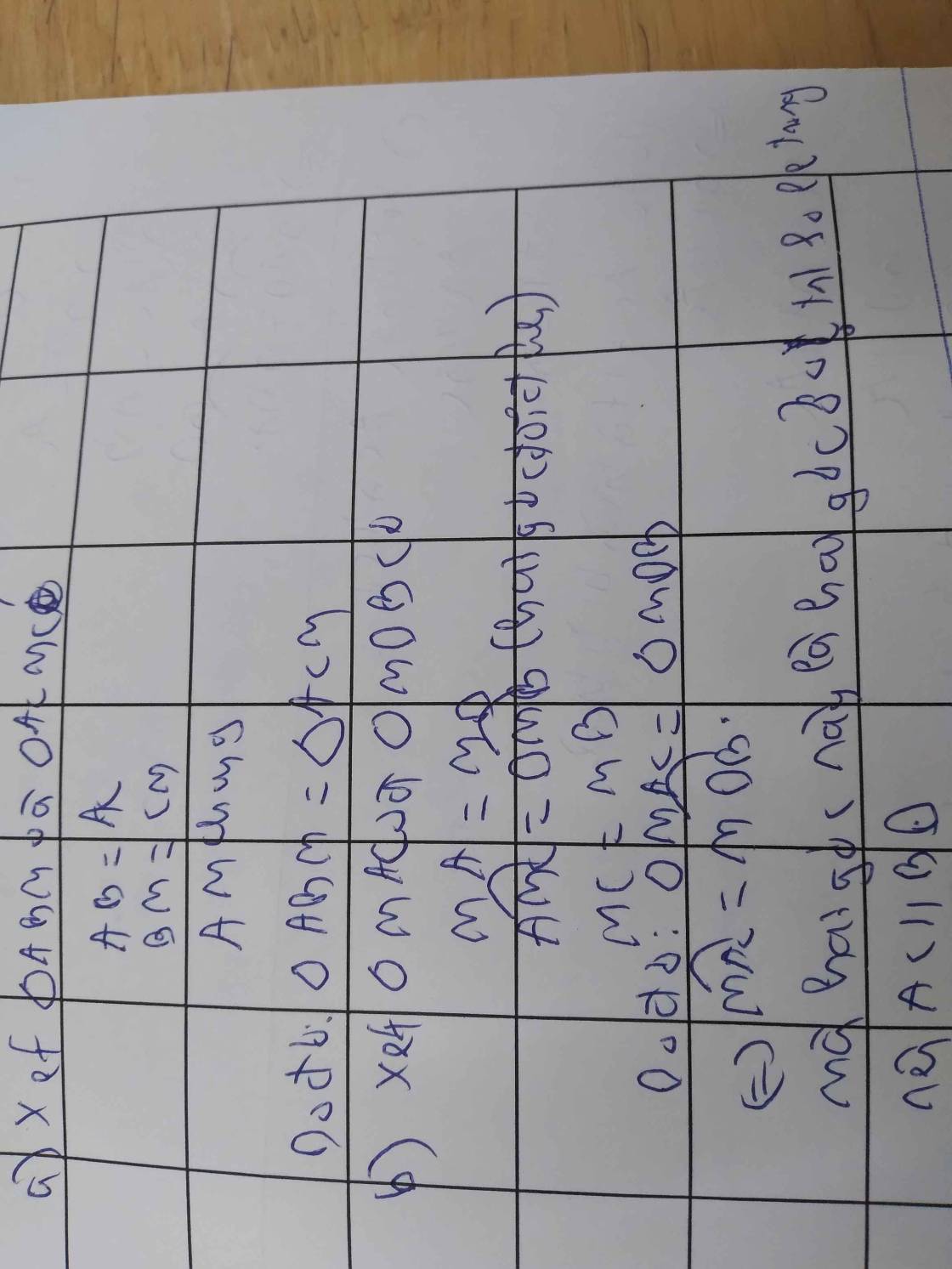

Sửa đề: MA=MK
a: Xét ΔMBK và ΔMCA có
MB=MC
\(\widehat{BMK}=\widehat{CMA}\)(hai góc đối đỉnh)
MK=MA
Do đó: ΔMBK=ΔMCA
=>BK=CA
mà AB=AC
nên BK=BA
=>ΔBAK cân tại B
b: Ta có: ΔMBK=ΔMCA
=>\(\widehat{MBK}=\widehat{MCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BK//AC