Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng: Δ ADC đối xứng với Δ AEB qua AH.

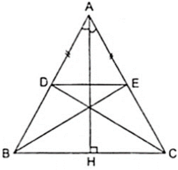
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.
Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE
⇒ D đối xứng với E qua AH.

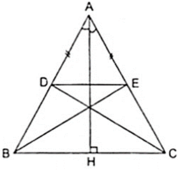
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.
⇒ B đối xứng với C qua AH, E đối xứng với D qua AH.
Mặt khác, ta có A đối xứng với A qua AH theo quy ước.
⇒ Δ ADC đối xứng với Δ AEB qua AH.

A B C D E M I
Bài làm
Gọi giao điểm của MA và ED là I
Xét tam giác cân ABC có:
=> \(\widehat{B}=\widehat{C}\)( hai góc ở đáy )
\(\Rightarrow\widehat{B}=\frac{180^0-\widehat{EAD}}{2}\) ( 1 )
Xét tam giác cân AED có: ( Vì EA = DA )
=> \(\widehat{E}=\widehat{D}\)
\(\Rightarrow\widehat{D}=\frac{180^0-\widehat{BAC}}{2}\)( 2 )
Mà \(\widehat{BAC}=\widehat{EAD}\)( Hai góc đối đỉnh )
Từ ( 1 ) và ( 2 ) => \(\widehat{B}=\widehat{D}\)
Mà hai góc này ở vị trí so le trong
=> ED // AM ( 3 )
Ta có: Tam giác ABC là tam giác cân.
Và M là trung điểm của BC
=> AM là đường trung tuyến của tam giác ABC
=> AM cũng là đường cao
=> AM | BC ( 4 )
Từ ( 3 ) và ( 4 ) => AI | ED
=> AI cũng là đường cao của ED
Và tam giác AED là tam giác cân
=> MA cũng là đường trung tuyến của của ED
=> EI = ID
=> E đối xứng với cả D qua AI
hay E đối xứng với D qua AM ( đpcm )
# Học tốt #

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

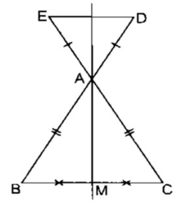
ΔABC cân tại A có AM là đường trung tuyến
⇒ AM là tia phân giác của góc (BAC)
⇒ ∠ (BAM) = ∠ (MAC) (1)
Kéo dài MA cắt DE tai N, ta có:
∠ (BAM) = ∠ (DAN) (đối đỉnh) (2)
∠ (MAC) = ∠ (NAE) (đối đỉnh)(3)
Từ (1), (2) và (3) suy ra: ∠ (DAN) = ∠ (NAE)
∆ ADE cân tại A có AN là tia phân giác
⇒ AN là đường trung trực của DE
hay AM là đường trung trực của DE
Vậy D đối xứng với E qua AM.

AD=ED
Định lí Talet đảo: \(\frac{AD}{AB}=\frac{AE}{AC}\Rightarrow DE//BC\)
Mà \(AH\perp BC\)nên \(AH\perp DE\)
Mà \(\Delta ADE\)cân tại \(A\)nên \(AH\)cũng là đường trung trực của \(DE\)
\(\Rightarrow D,E\)đối xứng nhau qua \(AH\)