Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

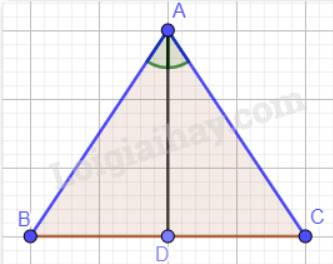
Xét hai tam giác ABD và ACD:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung.
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c).
Suy ra: BD = CD ( 2 cạnh tương ứng) hay D là trung điểm của cạnh BC. Vậy AD là đường trung tuyến của tam giác ABC.
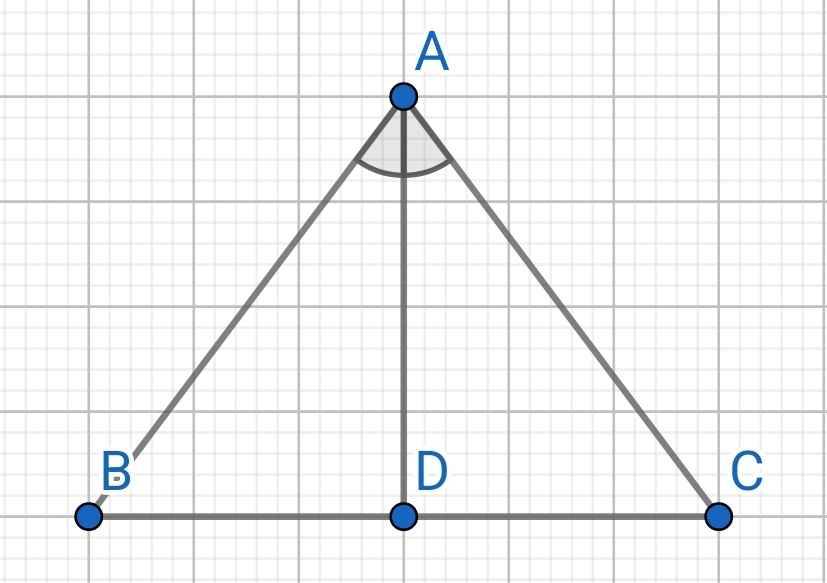 Do ∆ABC cân tại A
Do ∆ABC cân tại A
⇒ AB = AC và ∠ABC = ∠ACB
⇒ ∠ABD = ∠ACD
Do AD là đường phân giác của ∠BAC
⇒ ∠BAD = ∠CAD
Xét ∆ABD và ∆ACD có:
∠BAD = ∠CAD (cmt)
AB = AC (cmt)
∠ABD = ∠ACD (cmt)
⇒ ∆ABD = ∆ACD (g-c-g)
⇒ BD = CD (hai cạnh tương ứng)
⇒ D là trung điểm của BC
Vậy AD là đường trung tuyến của ∆ABC

vẽ hình ta thấy 0 là trục tâm vì là giao điiẻm của 2 đường cao nên o cách đều 3 đỉnh

a: Sửa đề: Chứng minh ΔABD=ΔAMD
Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: DB=DM
=>D nằm trên đường trung trực của BM(1)
ta có: AB=AM
=>A nằm trên đường trung trực của BM(2)
Từ (1),(2) suy ra AD là đường trung trực của BM

a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM

(Bạn tự vẽ hình giùm)
a/ \(\Delta BHD\)vuông và \(\Delta CKD\)vuông có: \(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A)
BD = CD (AD là đường trung tuyến của \(\Delta ABC\))
=> \(\Delta BHD\)vuông = \(\Delta CKD\)vuông (ch.gn) (đpcm)
b/ Ta có \(\Delta BHD\)= \(\Delta CKD\)(cmt) => BH = CK (hai cạnh tương ứng)
và AB = AC (\(\Delta ABC\)cân tại A)
=> AB - BH = AC - CK
=> AH = AK => \(\Delta AHK\)cân tại A (đpcm)
c/ Ta có \(\Delta AHK\)cân tại A (cmt) => \(\widehat{AHK}=\frac{180^o-\widehat{A}}{2}\)(1)
và \(\Delta ABC\)cân tại A (gt) => \(\widehat{B}=\frac{180^o-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AHK}=\widehat{B}\)ở vị trí đồng vị => HK // BC (đpcm)
d/ \(\Delta ADB\)và \(\Delta ADC\)có: AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A)
BD = CD (AD là đường trung tuyến của \(\Delta ABC\))
=> \(\Delta ADB\)= \(\Delta ADC\)(c. g. c) => \(\widehat{BAD}=\widehat{CAD}\)(hai góc tương ứng) => AD là đường phân giác của \(\Delta ABC\)(đpcm)
e/ Ta có \(\Delta ADB\)= \(\Delta ADC\)(cmt) =>\(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
Mà \(\widehat{ADB}+\widehat{ADC}=180^o\)(hai góc kề bù)
=> \(\widehat{ADB}=\widehat{ADC}=90^o\)=> AD \(\perp\)BC
và AD là đường trung tuyến của \(\Delta ABC\)
=> AD là đường trung trực của BC
Mà HK // BC
=> AD là đường trung trực của HK (đpcm)


AD là phân giác của góc A nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\);
AD chung
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c) nên \(BD = CD\) (2 cạnh tương ứng)
\(\Rightarrow\) D là trung điểm của cạnh BC.
Vì \(\Delta ABD = \Delta ACD\) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà \(\widehat {ADB} + \widehat {ADC}=180^0\) (2 góc kề bù) nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \Rightarrow AD \bot BC\).
Vậy AD là đường trung trực của tam giác ABC.