Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có AD = AE nên ∆ADE cân
Do đó ˆD1= ˆE1
Trong tam giác ADE có: D1^ + ˆE1 + ˆA^=1800
Hay 2ˆD1 = 1800 - ˆA
ˆD1 = 180 độ −ˆA/2
Tương tự trong tam giác cân ABC ta có ˆB= 180−ˆA/2
Nên ˆD1 = ˆB ( hai góc đồng vị.)
Suy ra DE // BC
Do đó BDEC là hình thang.
Lại có ˆB = ˆC
Nên BDEC là hình thang cân.
b) Với ˆA=500
Ta được ˆB = ˆC = 180−ˆA/2= 180-50/2=65 độ
ˆD2=ˆE2=1800 - ˆB= 1800 - 650=1150
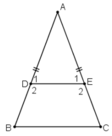
A B C D E 1 1 2 2
a) Ta có : AD = AE => \(\Delta ADE\)cân
\(\Rightarrow\widehat{D_1}=\widehat{E_1}\)
\(\Delta ADE\)có : \(\widehat{A}+\widehat{D_1}+\widehat{E_1}=180^o\)
Mà \(\widehat{D_1}=\widehat{E_1}\)nên \(\widehat{A}+2.\widehat{D_1}=180^o\)
\(\Rightarrow2.\widehat{D_1}=180^o-\widehat{A}\Rightarrow\widehat{D_1}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Tam giác ABC có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}=\widehat{C}\)( Vì tam giác ABC cân tại A )
\(\Rightarrow\widehat{A}+2.\widehat{B}=180^o\Rightarrow\widehat{B}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1)(2) => \(\widehat{D_1}=\widehat{B}\)
Mà hai góc ở vị trí đồng vị => DE // BC
=> Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
\(\widehat{A}=50^o\)thay vào (2) ta được :
\(\widehat{B}=\frac{180^o-50^o}{2}=65^o\)
Ta lại có : \(\widehat{B}=\widehat{C}\Rightarrow\widehat{C}=50^o\)
\(DE//BC\Rightarrow\widehat{D_1}+\widehat{B}=180^o\)
\(\Rightarrow\widehat{D_1}=180^o-\widehat{B}=115^o\)
DECB là hình thang cân
\(\Rightarrow\widehat{E_2}=\widehat{D_2}\Rightarrow\widehat{E_2}=115^o\)
Vậy : \(\widehat{B}=\widehat{C}=65^o\); \(\widehat{D_2}=\widehat{E_2}=115^o\)

Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
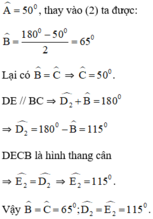

a) Ta xét: Tam giác ADE có: AD = AE
=> Tam giác ADE cân tại A
\(\Rightarrow\widehat{AED}=\widehat{ACB}\)
=> DE//BC
Ta xét: Tứ giác DECB có: DE//BC
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
=> BDEC là hình thang cân
b) \(\widehat{ABC}=\frac{1}{2}\left(180^o-50^o\right)=65^o\)
\(\widehat{ACB}=\widehat{ABC}=65^o\)
\(\widehat{DEC}=180^o-65^o=115^o\)
\(\widehat{EDB}=\widehat{EDC}=115^o\)
E C B D A

Hình vẽ:

a)Xét \(\Delta ADE\) có:AD=AE(gt)
\(\Rightarrow\Delta ADE\) cân tại A
\(\Rightarrow\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\) (1)
Ta lại có:\(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{AED}=\widehat{ACB}\)
\(\Rightarrow\) DE song song với BC
Xét tứ giác DEBC có:
DE song song với BC
\(\widehat{ABC}=\widehat{ACB}\) ( 2 góc đáy của tam giác ABC cân tại A)
\(\Rightarrow\) BDEC là hình thang cân
\(\Rightarrow\widehat{BDE}=\widehat{CED}\)
b) Theo câu a có:\(\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}=\dfrac{180^o-50^o}{2}=60^0\)
mà \(\widehat{ABC}=\widehat{ACB}\) ( câu a) nên \(\widehat{ABC}=60^o\)
Vì DE song song với BC\(\Rightarrow\) góc DEC+ góc BCE=180o
=>góc DEC+60o =180o
=>góc DEC=120o mà \(\widehat{BDE}=\widehat{CED}\)
=>BDE=120o

D E A B C
a) Ta có AD = AE nên ∆ADE cân
Do đó =
Trong tam giác ADE có: +
+
=1800
Hay 2 = 1800 -
=
Tương tự trong tam giác cân ABC ta có =
Nên =
là hai góc đồng vị.
Suy ra DE // BC
Do đó BDEC là hình thang.
Lại có =
Nên BDEC là hình thang cân.
b) Với =500
Ta được =
=
=
= 650
=1800 -
= 1800 - 650=1150

Thịnh có 15 hòn bi. Số bi của Thịnh hơn Khánh là 3 hòn. Nếu số bi của Huy thêm 4 hòn thì sẽ bằng số bi của Khánh. Hỏi cả ba bạn có bao nhiêu hòn bi.