Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vẽ tam giác EBC vuông cân tại E trong tam giác ABC
\(\widehat{EBC}=45^o\)
Ta có : EB2 + EC2 = BC2
2EB2 = 4 ; EB2 = 2 ; EB = \(\sqrt{2}\)
\(\Rightarrow\)EB = AD = \(\sqrt{2}\)
\(\Delta BAE\)= \(\Delta CAE\)( c.g.c ) suy ra : \(\widehat{BAE}=\widehat{CAE}=15^o\)
\(\widehat{ABC}=\left(180^o-30^o\right):2=75^o\)
\(\widehat{ABE}=75^o-45^o=30^o\)
\(\Rightarrow\)\(\widehat{ABE}=\widehat{BAD}=30^o\)
\(\Delta ABD=\Delta BAE\)( c.g.c ) suy ra : \(\widehat{ABD}=\widehat{BAE}=15^o\)
b) xét : \(\Delta DBC\)có : \(\widehat{DBC}=75^o-15^o=60^o\); \(\widehat{DCB}=75^o\)và \(\widehat{BDC}=45^o\)
suy ra : \(\widehat{BDC}< \widehat{DBC}< \widehat{DCB}\left(45^o< 60^o< 75^o\right)\)
Do đó : BC < CD < BD

A B C D E 1 1 1 2 2 1
\(\Delta ABC\)cân tại A nên\(\widehat{ABC}=\widehat{ACB}=\frac{180^0-\widehat{BAC}}{2}=75^0\)
Trên nửa mặt phẳng bờ BC chứa A lấy E sao cho\(\widehat{B_1}=\widehat{C_1}=45^0\)
=>\(\widehat{ABE}=75^0-45^0=30^0;\Delta EBC\)vuông cân tại E =>\(BE=EC=\frac{BC}{\sqrt{2}}=\sqrt{2}\left(cm\right)\)(định lí Pitago)
\(\Delta ABE,\Delta BAD\)có AB chung ; BE = AD\(\left(=\sqrt{2}cm\right)\);\(\widehat{ABE}=\widehat{BAD}\left(=30^0\right)\)
\(\Rightarrow\Delta ABE=\Delta BAD\left(c.g.c\right)\Rightarrow\widehat{A_1}=\widehat{B_2}\)
Lại có\(\Delta AEB=\Delta AEC\left(c.c.c\right)\)nên\(\widehat{A_1}=\widehat{A_2}=\frac{\widehat{BAC}}{2}=15^0\Rightarrow\widehat{B_2}=15^0\)
\(\Rightarrow\widehat{D_1}=\widehat{BAD}+\widehat{B_2}=45^0\)(\(\widehat{D_1}\)là góc ngoài\(\Delta ABD\)) ;\(\widehat{DBC}=75^0-15^0=60^0\)
\(\Delta BDC\)có\(\widehat{D_1}< \widehat{DBC}< \widehat{DCB}\left(45^0< 60^0< 75^0\right)\)nên BC < DC < BD

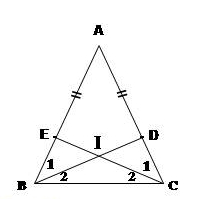
∆ABD và ∆ACE có:
AB=AC(gt)
ˆA góc chung.
AD=AE(gt)
Nên ∆ABD=∆ACE(c.g.c)
Suy ra: ˆABD=ˆACE.
Tức là ˆB1 =ˆC1
b) Ta có ˆB=ˆC mà ˆB1=ˆC1 suy ra ˆB2=ˆC2
Vậy ∆IBC cân tại I


Đường trung trực của cạnh BC cắt AB ở E.
Trên nửa mặt phẳng bờ CE không chứ A vẽ tam giác đều CEM
\(\widehat{ECB}=\widehat{EBC}=20^0;\widehat{BCM}=40^0\)
\(EB=EC=EM\Rightarrow\Delta EBM\)cân tại E
Ta có \(\widehat{BEM}=\widehat{BEC}-\widehat{MEC}=80^0\Rightarrow\widehat{EBM}=50^0\)
\(\Rightarrow\widehat{MBC}=30^0\)
Từ đó dễ dàng chứng minh \(\Delta CEA=\Delta MCB\left(g-c-g\right)\)
\(\Rightarrow AE=BC\)(hai cạnh tương ứng)
Mà BC = AD (gt) nên AD = AE \(\Rightarrow D\equiv E\)
\(\Rightarrow\widehat{BCD}=\widehat{BCE}=20^0\)
Vậy \(\widehat{BCD}=20^0\)
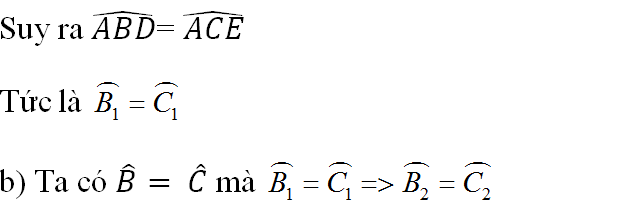
A B C E D
A) TRONG \(\Delta ABC\)TA VẼ \(\Delta EBC\)VUÔNG CÂN TẠI E;\(\widehat{EBC}=45^o\)
TA CÓ \(EB^2+EC^2=BC^2\)
\(2EB^2=4;EB^2=2;EB=\sqrt{2}\)
VẬY \(AD=EB=\sqrt{2}\)
\(\Delta BAE=\Delta CAE\left(C-G-C\right)\)
\(\Rightarrow\widehat{BAE}=\widehat{CAE}=15^o\)
\(\widehat{ABC}=\left(180^o-30^o\right):2=75^o;\widehat{ABE}=75^o-45^o=30^o;\)VẬY\(\widehat{ABE}=\widehat{BED}=30^o\)
\(\Delta ABD=\Delta BAE\left(C-G-C\right)\Rightarrow\widehat{ABE}=\widehat{BAE}=15^o\)
B)
\(\Delta DBC\)CÓ\(\widehat{DBC}=75^o-15^o=60^o;\widehat{DCB}=75^o\)VÀ\(\widehat{BDC}=45^o\)
\(\Rightarrow\widehat{BDC}< \widehat{DBC}< \widehat{DCB}\left(45^o< 60^o< 75^o\right)\)do đó BC<CD<BD( QUAN HỆ BA CẠNH VÀ GÓC ĐỐI DIỆN)
ᴾᴿᴼシĐệ❦℘ℛℴ༻꧂
-hình bạn vẽ thiếu dữ kiện nha
Tam giác ABC cân tại A , bạn phải kí hiệu AB=AC chứ