Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét tứ giác AKBC có
N là trung điểm của AB
N là trung điểm của CK
Do đó: AKBC là hình bình hành
Suy ra: AK=BC
hay AK=2MC
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
=>AM⊥BC
mà BC//AK
nên AM⊥AK
hay \(\widehat{MAK}=90^0\)

A C B M N K
a) Xét 2 tam giác ABM và ACM:
+ MB=MC
+ AB=AC
+ Cạnh AM chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
b) Xét 2 tam giác ANK và BNC
+ NK=NC
+ NA=NB
+ Góc ANK = góc BNC ( hai góc đối đỉnh )
\(\Rightarrow\Delta ANK=\Delta BNC\left(c.g.c\right)\)
\(\Rightarrow AK=BC\)( hai cạnh tương ứng )
Mà M là trung điểm của BC nên BC=2MC
\(\Rightarrow AK=2.MC\)
c) Ta có \(\widehat{AKN}=\widehat{BCN}\)( hai góc tương ứng của hai tam giác bằng nhau )
Mà hai góc AKN và BCN là cặp góc so le trong
\(\Rightarrow AK//BC\)
Vì hai tam giác ABM=ACM nên góc AMB= góc AMC ( hai góc tương ứng )
Mà góc AMB + AMC = 180 độ ( kề bù )\
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=90^o\)
\(\Rightarrow AM\perp BC\)
Mà AK//BC
\(\Rightarrow AM\perp AK\)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM

Bài 2
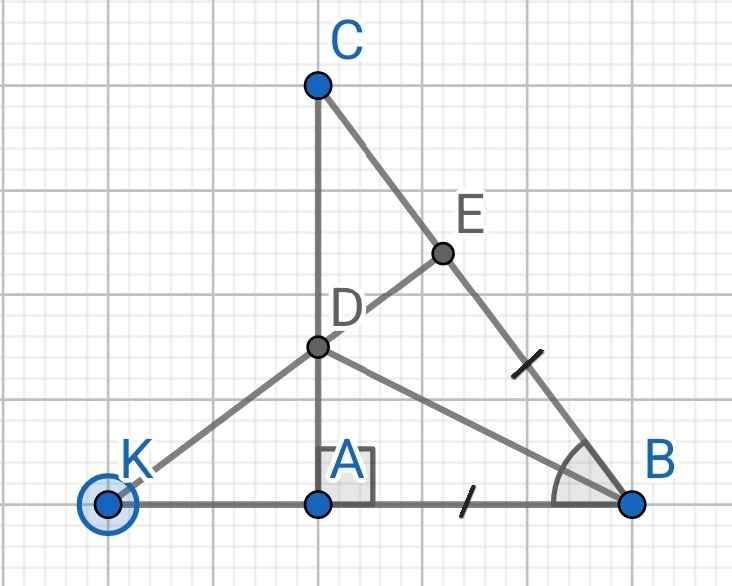
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (cmt)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ DE ⊥ BE
⇒ DE ⊥ BC
c) Do DE ⊥ BC (cmt)
⇒ ∠DEC = 90⁰
⇒ ∆DEC vuông tại E
Do ∆ABD = ∆EBD (cmt)
⇒ AD = DE (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ADK và ∆DEC có:
AD = DE (cmt)
∠ADK = ∠EDC (đối đỉnh)
⇒ ∆ADK = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AK = EC (hai cạnh tương ứng)
Ta có:
AB = BE (gt)
AK = EC (cmt)
⇒ AB + AK = BE + EC
⇒ BK = BC
Bài 1
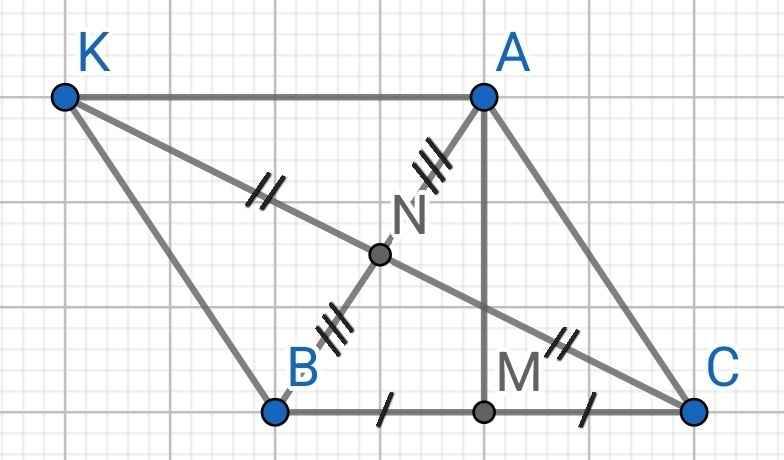 a) Xét ∆ABM và ∆ACM có:
a) Xét ∆ABM và ∆ACM có:
AM là cạnh chung
AB = AC (gt)
MB = MC (gt)
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do M là trung điểm của BC
⇒ BC = 2MC
Xét ∆ANK và ∆BNC có:
AN = BN (gt)
NK = NC (gt)
∠ANK = ∠BNC (đối đỉnh)
⇒ ∆ANK = ∆BNC (c-g-c)
⇒ AK = BC (hai cạnh tương ứng)
Mà BC = 2MC (cmt)
⇒ AK = 2MC
c) Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
⇒ ∆AMB vuông tại M
⇒ ∠ABM + ∠BAM = 90⁰ (1)
Do ∆ANK = ∆BNC (cmt)
⇒ ∠KAN = ∠NBC (hai góc tương ứng)
⇒ ∠KAN = ∠ABM (2)
Từ (1) và (2) ⇒ ∠MAK = ∠KAN + ∠BAM = 90⁰

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔNBC và ΔNAK có
NB=NA
\(\widehat{BNC}=\widehat{ANK}\)(hai góc đối đỉnh)
NC=NK
Do đó: ΔNBC=ΔNAK
=>BC=AK
mà BC=2MC
nên AK=2MC
c: ΔNBC=ΔNAK
=>\(\widehat{NBC}=\widehat{NAK}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BC//AK
ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
mà BC//AK
nên AM\(\perp\)AK
=>\(\widehat{KAM}=90^0\)

Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi

a.
Xét tam giác AHM và tam giác DCM có:
AM = DM (gt)
AMH = DMC (2 góc đối đỉnh)
MH = MC (M là trung điểm của HC)
=> Tam giác AHM = Tam giác DCM (c.g.c)
b.
AHM = DCM (tam giác AHM = tam giác DCM)
mà AHM = 90độ
=> DCM = 90độ
Tam giác ABC vuông tại A có:
ABC + ACB = 90độ
60độ + ACB = 90độ
ACB = 90 - 60
ACB = 30độ
ACD = ACB + DCM = 30 + 90 = 120độ
a) C/M tam giác AHM= tam giác DCM
Xét tam giác AHM và tam giác DCM, ta có:
MA=MD (gt)
góc AMH= góc DMC (đđ)
MH=MC (gt)
Vậy tam giác AHM= tam giác DCM (c-g-c)
b) Tính góc ACD
Ta có tam giác ABC vuông tại A có góc B=600 nên góc ACB=300
Lại có góc MCD= góc AHM = 900 (hai tam giác bằng nhau)
Vậy góc ACD= 300 + 900 = 1200
c) C/M AK=CD
Trong tam giác AHK, ta có AN đường cao đồng thời là trung tuyến ( AN vuông góc HK và NH=NK)
Nên tam giác AHK cân tại A
Suy ra AK=AH
Mà AH=CD (hai tam giác bằng nhau)
Vậy AK=CD
d) C/M K, H, D thẳng hàng
Ta có tam giác AHC= tam giác DCH ( c-g-c)
Nên góc ACH= góc DHC
Mà hai góc này ở vị trí so le trong
Suy ra AC//HD
Lại có HK//AC ( cùng vuông góc với AB)
Vậy K, H, D thẳng hàng

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b) xét ΔANK và ΔBNC, có:
NK = NC (gt)
\(\widehat{ANK}=\widehat{BNC}\) (đối đỉnh)
NB = NA (gt)
⇒ ΔANK = ΔBNC (c-g-c)
vì M là trung điểm của BC nên ta có: \(BC=MB+MC=2MC\)
mà KA = BC (2 cạnh tương ứng)
\(\Rightarrow BC=KA=2MC\)
c) ta có MB = MC (giả thiết)
⇒ MA là đường trung tuyến của ΔABC
⇒ MA cũng là đường phân giác của ΔABC
⇒ MA là đường phân giác của \(\widehat{BAC}\)
\(\widehat{BAC}=\widehat{BAM}+\widehat{MAC}=2\widehat{BAM}\\ \Rightarrow\widehat{BAM}=\dfrac{\widehat{BAC}}{2}=\dfrac{50^0}{2}=25^0\left(1\right)\)
Vì ΔABC cân tại A nên
\(\widehat{B}=\widehat{C}=\dfrac{\left(180^0-\widehat{A}\right)}{2}=\dfrac{\left(180^0-50^0\right)}{2}=\dfrac{130^0}{2}=65^0\)
mà \(\widehat{KAB}=\widehat{ABC}\) (2 góc tương ứng)
\(\Rightarrow\widehat{KAB}=65^0\left(2\right)\)
Từ (1) và (2) ta có:
\(\widehat{KAM}=\widehat{KAB}+\widehat{AMB}=65^0+25^0=90^0\)