Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A

a, Ta có ∆ABC cân ở A(gt)
AH\(\perp\) BC=>AH là đường cao
(1)=>AH đồng thời là trung tuyến=>HB=HC
(2)=>AH đồng thời là phân giác=>góc BAH=góc CAH
b, Áp dụng định lí pyta go cho ∆ABH ta có
AB2=AH2+BH2 =>52=42+HB2=>HB=√52--42=3
d, Xét ∆DHB và ∆EHC có
Góc HDB=góc HEC =90°(HD\(\perp\) AB, HE vuông góc ACgt)
Góc B=góc C ( tam giác ABC cân tai A gt)
HB =HC (cmt)
=> ∆DHB=∆EHC(ch-cgv)=>HD=HE=>∆HDE cân tại H

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC

a) Xét tam giác ABH và tam giác ACH có:
\(\widehat{AHB}=\widehat{AHC}=90^0\) (gt)
\(AB=AC\) (Do tam giác ABC cân tại A)
\(AH\) chung
\(\Rightarrow\Delta ABH=\Delta ACH\) (ch-cgv) \(\Rightarrow BH=CH\) (2 cạnh tương ứng)
b) Do \(\Delta ABH=\Delta ACH\Rightarrow\widehat{BAH}=\widehat{CAH}\) (2 góc tương ứng)
c) Do \(BH=CH\Rightarrow BH=CH=\dfrac{1}{2}BC=4\left(cm\right)\)
Áp dụng ĐL Pytago ta có: \(AB^2=AH^2+BH^2\)
\(5^2=AH^2+4^2\Rightarrow AH^2=5^2-4^2=9\Rightarrow AH=3\left(cm\right)\)

\(AH\perp BC\)
=> AH là đường cao của \(\Delta ABC\)
\(\Delta ABC\) cân tại A có AH là đường cao cũng là đường trung tuyến
\(\Rightarrow BH=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Xét \(\Delta HAB\) vuông tại H (AH là đường cao) có:
\(AB^2=AH^2+BH^2\left(Pytago\right)\\ \Rightarrow AH^2=AB^2-BH^2\\ \Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A

Hình vẽ:
A B C H 5cm 9cm 4cm
Xét \(\Delta ACH\left(\widehat{H}=90^0\right)\)có:
\(AC^2=AH^2+HC^2\)( định lý py-ta-go )
\(\Rightarrow5^2=4^2+HC^2\)
\(\Rightarrow HC^2=5^2-4^2\)
\(\Rightarrow HC^2=25-16\)
\(\Rightarrow HC^2=9\)
\(\Rightarrow HC=\sqrt{9}\)
\(\Rightarrow HC=3cm\)
Ta có: \(BH+HC=9cm\)
mà \(HC=3cm\left(cmt\right)\)
\(\Rightarrow BH=9-3=6cm\)
Xét \(\Delta AHB\left(\widehat{H}=90^0\right)\)có:
\(AB^2=AH^2+BH^2\)( định lý py-ta-go )
\(\Rightarrow AB^2=4^2+6^2\)
\(\Rightarrow AB^2=16+36\)
\(\Rightarrow AB^2=52\)
\(\Rightarrow AB=\sqrt{52}cm\)
Vậy độ dài cạnh AB là \(\sqrt{52}cm\)
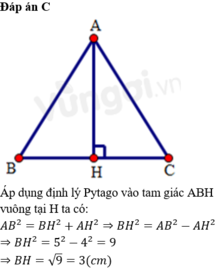
Cách 1: Dùng pytago với tgiác ABH => BH luôn
Cách 2: Dùng pytago với tgiác ACH => HC
Mà phải cm H là trung điểm BC nữa => HB. Nhưng cminh cũng không có gì khó khăn đâu mà
Nên tốt nhất bạn chọn cách 1 đi.
Vì \(AH⊥BC\Rightarrow\Delta AHB\) là tam giác vuông
Vì \(\Delta AHB\) vuông \(\Rightarrow AB^2=AH^{^{ }2}+BH^{^{ }2}\left(Py-ta-go\right)\)
hay \(^{5^2=4^2+BH^2}\)
\(5^2-4^2=BH^2\)
\(25-16=BH^2\)
\(9=BH^2\Rightarrow BH=\sqrt{9}\Rightarrow BH=3cm\)
Vậy BH=3cm