Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

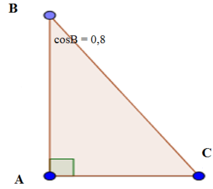
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
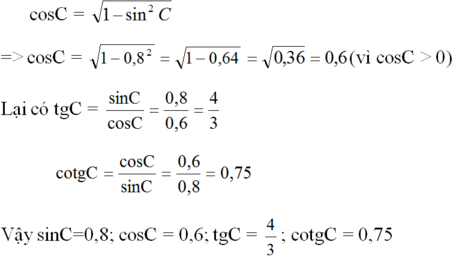

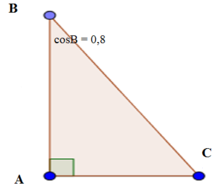
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
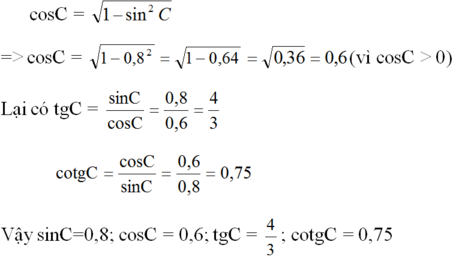

Bạn viết đề sai rồi
Cái \(3\dfrac{14}{17}\) là hỗn số chứ ko phải là số tự nhiên nhân vs phân số
#)Giải :
(Hình bn tự vẽ)
AD là phân giác của ∆ABC \(\Rightarrow\) \(\frac{BD}{AB}=\frac{DC}{AC}\Rightarrow\frac{BD^2}{AB^2}=\frac{DC^2}{AC^2}\)
Ta có : \(BC=BD+CD=3.\frac{14}{17}+9.\frac{3}{17}=\frac{42}{17}+\frac{27}{17}=\frac{69}{17}\)
Mà ∆ABC vuông tại A nên theo định lí Py - ta - go \(\Rightarrow AB^2+AC^2=BC^2\Rightarrow AB^2+AC^2=\left(\frac{69}{17}\right)^2\)
Theo t/chất dãy tỉ số bằng nhau : \(\frac{BD^2}{AB^2}=\frac{DC^2}{AC^2}=\frac{BD^2+DC^2}{AB^2+AC^2}=\frac{\left(\frac{42}{17}\right)^2+\left(\frac{27}{17}\right)^2}{\left(\frac{69}{17}\right)^2}=\) dài dòng vãi ra @@
Chắc đề sai rồi

a: \(\widehat{B}=60^0\)
AB=8cm
\(AC=4\sqrt{3}\left(cm\right)\)

A B C a 2a
Áp dụng định lí Pi-ta-go cho \(\Delta ABC\)vuông tại A, ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=4a^2-a^2\)
\(\Leftrightarrow AC=\sqrt{3a^2}=a\sqrt{3}\)
a) Tỉ số lượng giác của góc B là:
\(\sin B=\frac{a\sqrt{3}}{2a}=\frac{\sqrt{3}}{2}\)
\(\cos B=\frac{a}{2a}=\frac{1}{2}\)
\(\tan B=\frac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\cot B=\frac{a}{a\sqrt{3}}=\frac{1}{\sqrt{3}}\)
b) Tỉ số lượng giác của góc C là:
\(\sin C=\cos B=\frac{1}{2}\)( Định lí )
\(\cos C=\sin B=\frac{\sqrt{3}}{2}\)( Định lí )
\(\tan C=\cot B=\frac{1}{\sqrt{3}}\)( Định lí )
\(\cot C=\tan B=\sqrt{3}\)( Định lí )
Chúc bn hok tốt

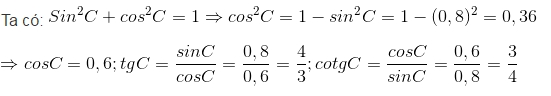
Bạn tự vẽ hình nha
Từ A hạ AH vuông góc với BC
Ta có tam giác ABC là tam giác cân có
AH là đường cao
=>AH là đường phân giác và là đường trung trực
=>+)Góc BAH=Góc HAC = Góc BAC/2=20°/2=10°
+)HB=HC=BC/2=2/2=1
Theo tỉ số lượng giác trong tam giác AHB vuông tại H có:
Sin BAH=BH/AB
Sin10°=1/AB
<=>AB=1/Sin10°
<=> AB=5.76 cm
~Chúc bạn học tốt~