Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

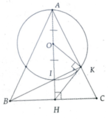
a, Chứng minh được B K A ^ = 90 0
b, Gọi O là trung điểm AI
Ta có:
+ OK = OA => O K A ^ = O A K ^
+ O A K ^ = H B K ^ (cùng phụ A C B ^ )
+ HB = HK => H B K ^ = H K B ^
=> O K A ^ = H K B ^ ⇒ H K O ^ = 90 0

a: Vì góc AKI=90 độ
nên K nằm trên đường tròn đường kính AI
b: Gọi G là trung điểm của AK
góc GKH=góc GKI+góc HKI
=góc GIK+góc HBI
=góc BIH+góc HBI=90 độ
=>HK là tiếp tuyến của (G)

Đáp án A
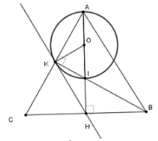
Gọi O là trung điểm AI. Xét tam giác vuông AIK có
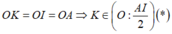
Xét tam giác OKA cân tại O (vì OA=OK=R) có:
O K A ^ = O A K ^ (1)
Xét tam giác CKB vuông tại K (vì K B ⊥ A C ) có:
H là trung điểm CB (vì tam giác ABC cân tại A có AH là đường cao nên đồng thời là đường trung tuyến)
⇒ KH là trung tuyến ứng với cạnh huyền BC
⇒ H K C ^ = H C K ^ ( 2 )
Từ (1) và (2) suy ra O K A ^ + H K C ^ = O A K ^ + H C K ^ = 90 o (vì A H ⊥ B C )
Mà O K A ^ + H K C ^ + O K H ^ = 180 o ⇒ O K H ^ = 90 o ⇒ O K ⊥ K H (**)
Từ (*) và (**) suy ra HK là tiếp tuyến của (O)

Chọn đáp án A
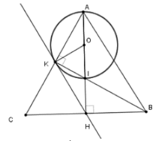
Gọi O là trung điểm AI. Xét tam giác vuông AIK có
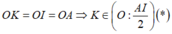
Từ (*) và (**) thì HK là tiếp tuyến của đường tròn đường kính AI

a: Ta có: ΔBKC vuông tại K
mà KH là trung tuyến
nên KH=BH
=>ΔHBK cân tại H
b: góc BAH=90 độ-góc ABC
góc IAK=90 độ-góc ACB
mà góc ABC=góc ACB
nên góc BAH=góc IAK
c: Gọi G là trung điểm của AI
góc GKH=góc GKI+góc HKI
=góc GIK+góc HBI
=góc BIH+góc HBI=90 độ
=>HK là tiếp tuyến của (G)


hình bạn tự kẻ nha
a> Xét tam giác ADE và tam giác AHB có : góc DAE = HAB(đối đỉnh); góc ADE = góc AHB = 90 độ; AD = AH = bán kính==> tg ADE = AHB (c.g.v_g.n.k)
b> vì tg ADE = AHB ==> AE = AB ==> A là trung điểm của BE (1)
xét tg CBE ta thấy CA vuông góc với AB ==> CA là đường cao (2)
từ (1) và (2) ==> tg CBE cân tại C
c> vì tg CBE cân tại C ==> CA vừa là đường cao vừa là tia pg xuất phát từ đỉnh C ==> góc ACH = ACI
xét tg ACH và tg ACI có: góc AHC = AIC = 90 độ; AC là cạnh chung; góc ACH = ACI(cmt) ==> tg ACH = ACI (c.h_g.n)
=> AH=AI=bán kính (3)
mặt khác AI vuông góc với CE (4)
từ (3) và (4) ==> CE là tiếp tuyến ( khoảng cách từ tâm đến đường thẳng bằng bán kính)
a: Vì góc AKI=90 độ
nên K nằm trên đường tròn đường kính AI
b: Gọi G là trung điểm của AK
góc GKH=góc GKI+góc HKI
=góc GIK+góc HBI
=góc BIH+góc HBI=90 độ
=>HK là tiếp tuyến của (G)