Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 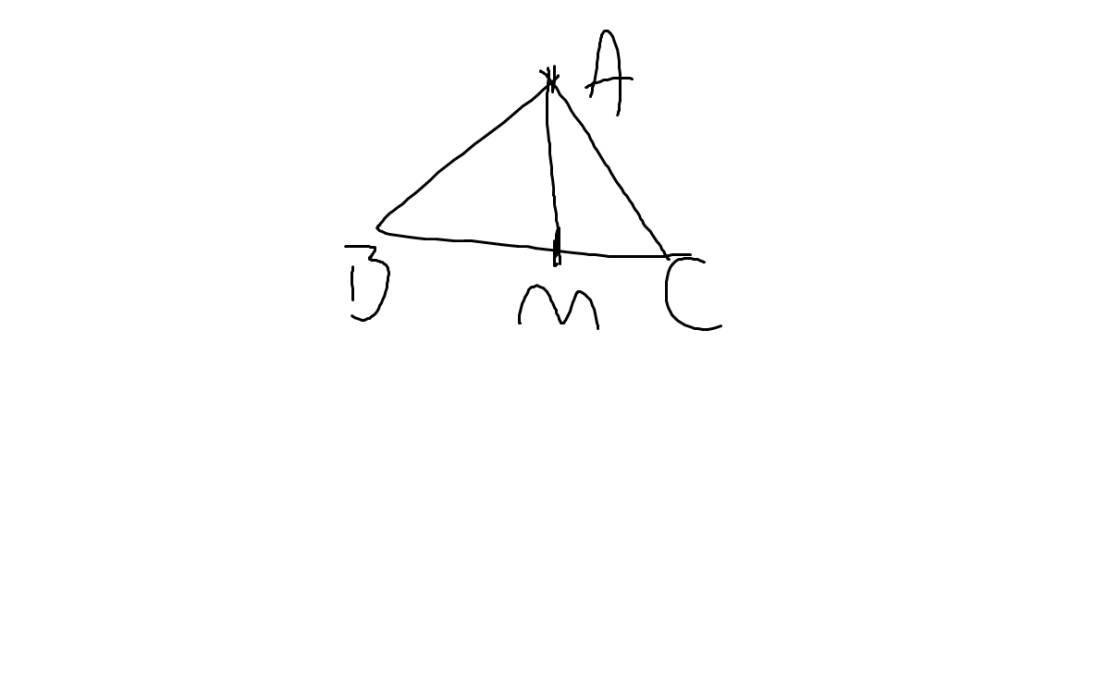
b: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC

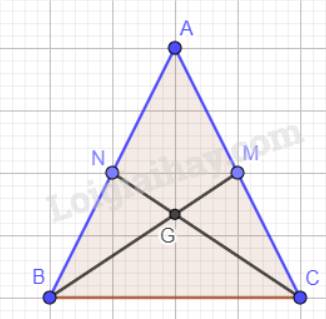
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.
Xét tam giác ABM và tam giác ACN có: AM = AN; \(\widehat A\)chung; AB = AC.
Vậy \(\Delta ABM = \Delta ACN\)(c.g.c) hay BM = CN.
b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Do đó:
\(GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN\). Mà BM = CN nên GB = GC.
Vậy tam giác GBC cân tại G.

a: Xét ΔBNC và ΔCMB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó; ΔBNC=ΔCMB
b: Sửa đề: Cm ΔANM cân tại A
Xét ΔANM có AN=AM
nên ΔANM cân tại A

a) Sửa đề: Cm AG vuông góc với BC
Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AN=NB=AM=MC
Xét ΔNBC và ΔMCB có
NB=MC(cmt)
\(\widehat{NBC}=\widehat{MCB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔNBC=ΔMCB(c-g-c)
Suy ra: \(\widehat{NCB}=\widehat{MBC}\)(hai góc tương ứng)
hay \(\widehat{GBC}=\widehat{GCB}\)
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)(cmt)
nên ΔGBC cân tại G(Định lí đảo của tam giác cân)
Suy ra: GB=GC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: GB=GC(cmt)
nên G nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AG là đường trung trực của BC
hay AG\(\perp\)BC(đpcm)

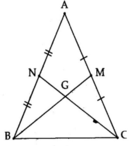
Sửa đề: đường trung tuyến CM
Xét ΔABC có BN,CM là các đường trung tuyến
BN cắt CM tại G
Do đó: G là trọng tâm của ΔABC
=>G thuộc đường trung tuyến xuất phát từ đỉnh A