K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

27 tháng 7 2016
đừng tích ai nhá, tôi về mình giải cho, giờ mik phải đi học thêm

CM
30 tháng 7 2018
+) Ta có:
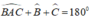 (tổng ba góc trong 1 tam giác)
(tổng ba góc trong 1 tam giác)
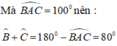
Lại có: tam giác ABC là tam giác cân tại A nên:
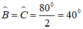
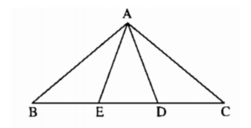
+)Xét tam giác ABD có BA= BD (giả thiết) nên tam giác ABD cân tại B.
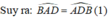
Lại có; 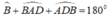 ( tổng ba góc trong 1 tam giác)
( tổng ba góc trong 1 tam giác)
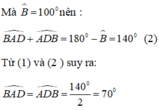
+) Tương tự, ta có tam giác AEC cân tại C ( vì CA =CE)
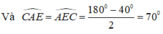
+) Xét tam giác ADE có:
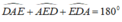 ( tổng ba góc trong tam giác)
( tổng ba góc trong tam giác)
Suy ra:
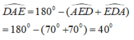

26 tháng 12 2015
- Đây nè bạn ~> http://olm.vn/hoi-dap/question/130302.html
- Tick cho mềnh nha ^^~
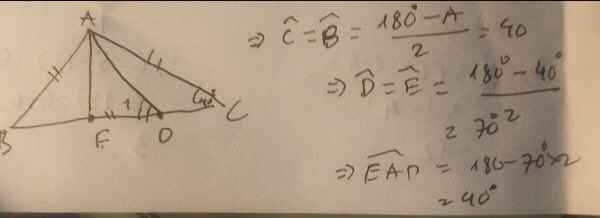
\(\Delta\)ABC cân tại A nên \(\widehat{B}=\widehat{C}\)
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(định lí)
mà \(\widehat{B}=\widehat{C}\)
=> \(\widehat{A}+2\widehat{B}=180^0\)
=> \(\widehat{A}=180^0-2\widehat{B}\)
=> \(180^0-2\widehat{B}=80^0\)
=> \(2\widehat{B}=100^0\)
=> \(\widehat{B}=50^0\)
Do đó \(\widehat{B}=\widehat{C}=50^0\)
Ta có : BD = BA => \(\Delta\)ABD cân tại B => \(\widehat{BAD}=\widehat{BDA}\)
\(\widehat{BAD}=\widehat{BDA}=\frac{180^0-\widehat{B}}{2}=\frac{180^0-50^0}{2}=65^0\)
=> \(\widehat{BAD}=65^0\)
CE = CA => \(\Delta\)ACE cân tại C => \(\widehat{CAE}=\widehat{CEA}\)
Do đó \(\widehat{CAE}=\widehat{CEA}=\frac{180^0-\widehat{C}}{2}=\frac{180^0-50^0}{2}=65^0\)
=> \(\widehat{CAE}=65^0\)
Xét \(\Delta\)DAE theo định lí tổng ba góc trong 1\(\Delta\))
=> \(\widehat{BAD}+\widehat{CAE}+\widehat{DAE}=180^0\)
=> \(65^0+65^0+\widehat{DAE}=180^0\)
=> \(\widehat{DAE}=180^0-130^0=50^0\)
Vậy \(\widehat{DAE}=50^0\)
Góc DAE = 80 độ