Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Suy ra: \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
hay \(\widehat{ADM}=90^0\)
Xét ΔADM có DA=DM(gt)
nên ΔADM cân tại D(Định nghĩa tam giác cân)
Xét ΔADM cân tại D có \(\widehat{ADM}=90^0\)(cmt)
nên ΔADM vuông cân tại D(Định nghĩa tam giác vuông cân)

Trả lời:
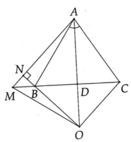
A B C D M N O
a, Tam giác ABC cân tại A có: AD là đường phân giác của ^BAC
=> AD đồng thời là đường trung trực của của tam giác ABC
=> AD \(\perp\)BC
=> tam giác DAM vuông tại D (đpcm)
b, Xét tam giác AMO có:
ON là đường cao thứ nhất ( ON \(\perp\)AM )
MD là đường cao thứ hai ( MD \(\perp\)AO )
Mà ON và BN cắt nhau tại B
=> B là trực tâm của tam giác AMO
=> AB là đường cao thứ ba
=> AB \(\perp\)OM (đpcm)
c, Tam giác BCO có:
AD là đường trung trực hay OD là đường trung trực ứng với canh BC
=> O cách đều 2 đầu mút B và C
=> OB = OC (đpcm)

a) Xét ΔAFC vuông tại F và ΔAFD vuông tại F có
AC=AD(=AB)
AF chung
Do đó: ΔAFC=ΔAFD(Cạnh huyền-cạnh góc vuông)
Suy ra: FC=FD(hai cạnh tương ứng)
mà C,F,D thẳng hàng(gt)
nên F là trung điểm của CD
Xét ΔBCD có
CA là đường trung tuyến ứng với cạnh BD(gt)
BF là đường trung tuyến ứng với cạnh DC(cmt)
CA cắt BF tại G(gt)
Do đó: G là trọng tâm của ΔBDC(Tính chất ba đường trung tuyến của tam giác)
\(\Leftrightarrow AG=\dfrac{1}{3}AC\)(Tính chất trọng tâm của tam giác)
mà \(AC=\dfrac{1}{2}BD\left(=AB\right)\)
nên \(AG=\dfrac{1}{3}\cdot\dfrac{1}{2}BD=\dfrac{1}{6}BD\)
hay BD=6AG(đpcm)

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
b:
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>góc HBD=góc KCE
=>góc IBC=góc ICB
=>ΔIBC cân tại I
c: Xét ΔABI và ΔACI có
AI chung
AB=AC
BI=CI
=>ΔABI=ΔACI
=>góc BIA=góc CIA
=>IA là phân giác của góc BIC

xét tam giác ABC cân tại A có
AD là phân giác
=> AD là đg cao (tc tam giác cân )
=>AD⊥BC
=> AD⊥DC (D ∈ BC)=> AD⊥MD (M∈DC)
xét tam giác ADM có
MD = AD (gt)
AD⊥MD
=> tam giác ADM vuông cân tại D