Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

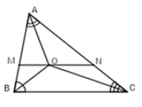
Vì OM//BC nên \(\widehat{MOB}=\widehat{MBO}\)
Ví ON//BC nên\(\widehat{ONC}=\widehat{OCN}\)
Xét \(\Delta BOM\)có \(\widehat{MOB}=\widehat{MBO}\)=> \(\Delta BOM\)cân (t/c)=> MB=MO
Xét \(\Delta OCN\)có \(\widehat{ONC}=\widehat{OCN}\)=> \(\Delta OCN\)cân (t/c)=> ON=NC
Ta lại có MO+ON=MN
=> BM+CN=MN (đpcm)
Vì OM // BC nên \(\widehat{MOB}\)= \(\widehat{MBO}\)
Vì ON // BC nên \(\widehat{ONC}\)= \(\widehat{OCN}\)
Xét \(\Delta BOM\)có \(\widehat{MOB}\)= \(\widehat{MBO}\)=> \(\Delta BOM\)cân (t/c) => MB = MO
Xét \(\Delta OCN\)có \(\widehat{ONC}\)= \(\widehat{OCN}\)=> \(\Delta OCN\)cân (t/c) => ON = NC
Ta có MO + ON = MN
=> BM + CN = MN ( đpcm )

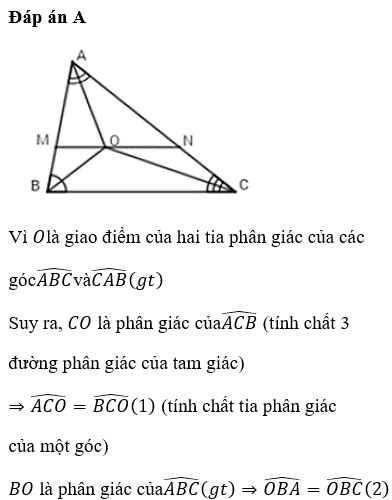
a) Ta có: EF//BC(gt) =>\(\left\{{}\begin{matrix}\text{^EOB = ^OBC (SLT)}\\\text{ ^FOC = ^OCB (SLT)}\\\text{^AEF = ^B (Đồng vị)}\\\text{^AFE = ^C (Đồng vị)}\end{matrix}\right.\)
Có: ^OBC = ^OBA ( BF là phân giác ^B)
mà: ^EOB = ^OBC (cmt)
=> ^EOB = ^OBA => tam giác EBO cân tại E
Có: ^OCA = ^OCB ( BF là phân giác ^B)
mà: ^FOC = ^OCB (cmt)
=> ^FOC = ^OCA => tam giác FCO cân tại E
Ta có: ^AEF = ^B (cmt)
^AFE = ^C (cmt)
Mà ^B = ^C (tam giác ABC cân tại A)
=> ^AEF = ^AFE => tam giác AEF cân tại A
Có : ^ABF = ^CBF = \(\dfrac{1}{2}\) ^B ( BF là phân giác ^B)
^ACE = ^BCE = \(\dfrac{1}{2}\) ^B ( CF là phân giác ^C)
mà : ^B = ^C (tam giác ABC cân tại A)
=> ^ACE = ^ABF = ^CBF = ^BCE
Xét tg OBC có: ^OBC = ^OCB (^CBF = ^BCE) => tg OBC cân tại O
Xét tam giác FCO và tam giác EBO có:
^FOC = ^FOB ( đối đỉnh)
^FCO = ^EBO (^ABF = ^ACE)
OB = OC ( tg OBC cân tại O )
=> tam giác FCO = tam giác EBO(g-c-g)



úi lụn bai ko xóa ik dc
MN = 3+4 =7 (cm)