Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=3,6(cm)

Lời giải:
Ta thấy \(6^2+4,5^2=7,5^2\)
\(\Leftrightarrow AB^2+AC^2=BC^2\)
Theo định lý Pitago đảo thì tam giác $ABC$ vuông tại $A$
Với tam giác $ABC$ vuông tại $A$:
\(S_{ABC}=\frac{AH.BC}{2}=\frac{AB.AC}{2}\Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.4,5}{7,5}=3,6\) (cm)
b)
Áp dụng định lý Pitago cho tam giác $AHB$
\(BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-3,6^2}=4,8\) (cm)
\(CH=BC-BH=7,5-4,8=2,7\) (cm)

a: Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔBAC vuông tại A
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH=\dfrac{4\cdot5\cdot6}{7.5}=3.6\left(cm\right)\)
c: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{6^2}{7.5}=4.8\left(cm\right)\\CH=\dfrac{4.5^2}{7.5}=2.7\left(cm\right)\end{matrix}\right.\)

mình chỉ biết bài 3 thôi. hai bài kia cx làm được nhưng ngại trình bày
A B C 4 9
Ta có : BC = BH +HC = 4 + 9 = 13 (cm)
Theo hệ thức lượng trong tam giác vuông ta có:
- AC2 = BC * HC
AC2 = 13 * 9 = 117
AC = \(3\sqrt{13}\)(cm)
- AB2 =BH * BC
AB2 = 13 * 4 = 52
AB = \(2\sqrt{13}\)(CM)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=3,6(cm)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)

a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
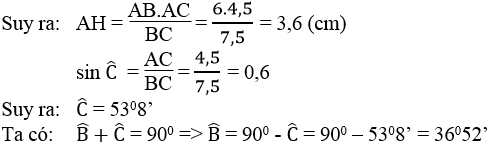 b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.

Nếu BC2 = AC2 + AB2 thì tam giác ABC vuông tại A. (Pytago)
ta có: 7,52 = 4,52 + 62 => tam giác ABC vuông tại A.
Tam giác ABC vuông tại A, đường cao AH nên: AH.BC = AC.AB <=> AH = (AC.AB)/BC <=> AH = 3,6 cm
Ta có: AB2 = BC.BH <=> BH = AB2 /BC <=> 36/7,5 = 4,8 cm
=> HC = BC - BH = 7.5 - 4.8 = 2.7 cm
vẽ hình nữa nha