E
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
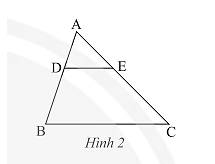
Xét tam giác \(ABC\) có \(DE//BC\) nên theo định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}} \Rightarrow \frac{x}{2} = \frac{6}{3}\). Do đó, \(x = \frac{{6.2}}{3} = 4\).
Vậy \(x = 4\).
25 tháng 8 2021
a: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{BM}=\dfrac{4}{6}=\dfrac{2}{3}\)
b: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\left(1\right)\)
Xét ΔAMC có
ME là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)
Ta có: M là trung điểm của BC
nên MB=MC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
c: Xét ΔABC có
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
Vì \(DE//BC\) nên theo định lí Thales và hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\frac{{BD}}{{AD}} = \frac{{EC}}{{AE}};\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
18 tháng 2 2023
a: Xét ΔIAB có ID là phân giác
nên DA/DB=AI/IB=AI/IC
Xét ΔIAC có IE là phân gíac
nên AE/EC=AI/IC
=>DA/DB=EA/EC
=>DE//BC
b: Xét ΔABI có DO//BI
nên DO/BI=AO/AI
Xét ΔACI co EO//IC
nên EO/IC=AO/AI
=>DO/BI=EO/IC
mà BI=IC
nên DO=EO
=>O là trung điểm của DE