Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Đường thẳng qua điểm M và có véc tơ chỉ phương là vecto tích có hướng của vecto chỉ phương của đường thẳng d và vecto pháp tuyến của mặt phẳng (P).

A B C E K
a) Xét \(\Delta AKB\) và \(\Delta AKC\) , có :
AK là cạnh chung
AB = AC ( gt )
BK = KC ( K là trung điểm của BC )
=> \(\Delta AKB=\Delta AKC\left(cgc\right)\)
Ta có :
+ Góc AKB = AKC ( \(\Delta AKB=\Delta AKC\) )
Mà góc AKB + AKC = 1800 ( 2 góc kề bù )
=> AKB = AKC= \(\frac{180^0}{2}\)= 900
Vậy AK \(\perp BC\)
b)
Ta có :
AK \(\perp BC\) ( Theo câu a )
EC \(\perp BC\) ( gt )
=> EC // AK
c) Tam giác BCE là tam giác vuông
GÓC BEC = 500

Chọn đáp án D
Ta có
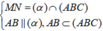
![]()
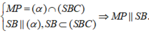
![]()
Khi đó ![]()
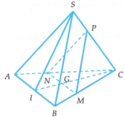
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
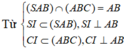
![]()
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
![]()
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0

Chọn A
Ta có trung điểm của đoạn thẳng AB là điểm I(0;1;-1). Đường thẳng d có vecto chỉ phương là u=(1;-1;2). Vậy phưng trình đường thẳng đi qua trung điểm của đoạn thẳng
AB và song song với d là:
![]()