Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ABCEHD
+) Kẻ AE là phân giác ngoài của góc BAC
Mà AD là phân giác của góc BAC nên AD vuông góc với AE => tam giác EAD vuông tại A
+) Áp dụng ĐL Pi - ta go trong tam giác vuông AHD có: DH = √AD2−AH2=√452−362=27 cm
+) Áp dụng hệ thức lượng trong tam giác vuông EAD có: AD2 = DH. DE => DE = AD2 / DH = 452/ 27 = 75 cm
+)Áp dụng tính chất tia phân giác trong và ngoài tam giác có: BDDC =ABAC =EBEC
Đặt BD = x (0 < x < 40) => CD = 40 - x. Ta có:
x40−x =75−x75+(40−x) (do EB = DE - BD; EC = DE + DC)
=> x. (115 - x) = (40 - x).(75 - x)
<=> 115x - x2 = 3000 - 115x + x2 <=> x2 - 115x + 1500 = 0
=> x = 100 (Loại) hoặc x = 15 (thoả mãn)
Vậy BD = 15 cm hoặc BD = 40 - 15 = 25 cm (Nếu ta đổi vị trí B và C cho nhau)

Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=10.tan45^0=10\)
\(cosB=\dfrac{BH}{AB}\Rightarrow AB=\dfrac{BH}{cosB}=\dfrac{10}{cos45^0}=10\sqrt{2}\)
Do tam giác ABH vuông tại H \(\Rightarrow\widehat{BAH}=90^0-\widehat{B}=45^0\)
\(\Rightarrow\widehat{CAH}=\widehat{A}-\widehat{BAH}=75^0-45^0=30^0\)
Trong tam giác vuông ACH:
\(cos\widehat{CAH}=\dfrac{AH}{AC}\Rightarrow AC=\dfrac{AH}{cos\widehat{CAH}}=\dfrac{10}{cos30^0}=\dfrac{20\sqrt{3}}{3}\)
AD là phân giác góc A \(\Rightarrow\widehat{CAD}=\dfrac{1}{2}\widehat{A}=\dfrac{75^0}{2}=37^030'\)
\(\Rightarrow\widehat{DAH}=\widehat{CAD}-\widehat{CAH}=37^030'-30^0=7^030'\)
Trong tam giác vuông ADH:
\(cos\widehat{DAH}=\dfrac{AH}{AD}\Rightarrow AD=\dfrac{AH}{cos\widehat{DAH}}=\dfrac{10}{cos\left(7^030'\right)}\approx10,1\)

3:
Đặt HB=x; HC=y
Theo đề, ta có: x+y=289 và xy=120^2=14400
=>x,y là các nghiệm của phương trình:
a^2-289a+14400=0
=>a=225 hoặc a=64
=>(x,y)=(225;64) và (x,y)=(64;225)
TH1: BH=225cm; CH=64cm
=>\(AB=\sqrt{225\cdot289}=15\cdot17=255\left(cm\right)\) và \(AC=\sqrt{64\cdot289}=7\cdot17=119\left(cm\right)\)
TH2: BH=64cm; CH=225cm
=>AB=119m; AC=255cm

1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{6}=\dfrac{CD}{8}\)
mà BD+CD=10cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{6}=\dfrac{CD}{8}=\dfrac{BD+CD}{6+8}=\dfrac{10}{14}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{30}{7}cm;CD=\dfrac{40}{7}cm\)

1)
a) Xét ΔABC có
\(BC^2=AC^2+AB^2\left(7.5^2=4.5^2+6^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A, ta được:
\(AB\cdot AC=AH\cdot BC\)
\(\Leftrightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{4.5\cdot6}{7.5}=\dfrac{27}{7.5}=3.6\left(cm\right)\)
Vậy: AH=3,6cm
b) Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow CH^2=4.5^2-3.6^2=7.29\)
hay CH=2,7(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BH=BC-CH=7,5-2,7=4,8(cm)
Vậy: BH=4,8cm; CH=2,7cm
1.a)Ta có:7,52=4,52+62 nên theo định lí Py-ta-go
=>\(\Delta ABC\) vuông tại A
Ta có: AB.AC=BC.AH
=> \(AH=\dfrac{AC.AB}{BC}=\dfrac{4,5.6}{7,5}=3.6\) (cm)
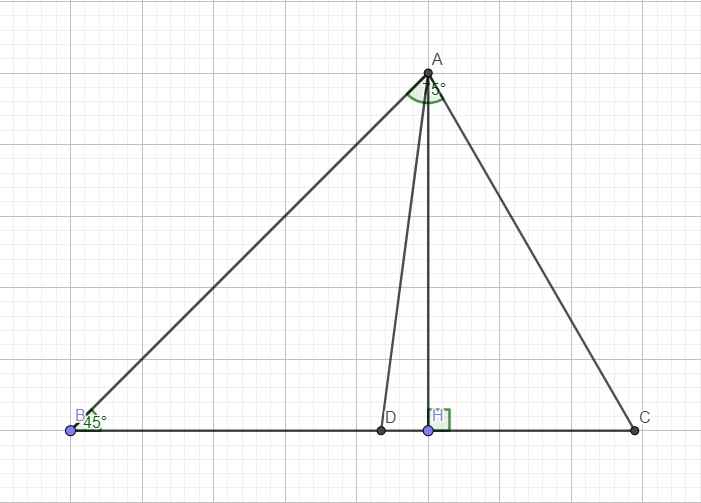
ABCEHD
+) Kẻ AE là phân giác ngoài của góc BAC
Mà AD là phân giác của góc BAC nên AD vuông góc với AE => tam giác EAD vuông tại A
+) Áp dụng ĐL Pi - ta go trong tam giác vuông AHD có: DH = √AD2−AH2=√452−362=27 cm
+) Áp dụng hệ thức lượng trong tam giác vuông EAD có: AD2 = DH. DE => DE = AD2 / DH = 452/ 27 = 75 cm
+)Áp dụng tính chất tia phân giác trong và ngoài tam giác có: BDDC =ABAC =EBEC
Đặt BD = x (0 < x < 40) => CD = 40 - x. Ta có:
x40−x =75−x75+(40−x) (do EB = DE - BD; EC = DE + DC)
=> x. (115 - x) = (40 - x).(75 - x)
<=> 115x - x2 = 3000 - 115x + x2 <=> x2 - 115x + 1500 = 0
=> x = 100 (Loại) hoặc x = 15 (thoả mãn)
Vậy BD = 15 cm hoặc BD = 40 - 15 = 25 cm (Nếu ta đổi vị trí B và C cho nhau)