Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Xét tam giác $AMC$ và $EMB$ có:
$AM=ME$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{AMC}=\widehat{EMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle EMB$ (c.g.c)
$\Rightarrow AC=EB$
b. Xét tam giác $AFD$ và $BED$ có:
$FD=ED$
$AD=BD$ (do $D$ là trung điểm $AB$)
$\widehat{ADF}=\widehat{BDE}$ (đối đỉnh)
$\Rightarrow \triangle AFD=\triangle BED$ (c.g.c)
$\Rightarrow AF=BE$
Mà theo phần a thì $AC=BE$ nên $AF=AC$

Bạn tự vẽ hình nha![]()
a.
Xét tam giác MBE và tam giác MCA có:
MB = CM (AM là trung tuyến của tam giác ABC => M là trung điểm của BC)
BME = CMA (2 góc đối đỉnh)
AM = EM (gt)
=> Tam giác MBE = Tam giác MCA (c.g.c)
=> BE = CA (2 cạnh tương ứng)
=> MEB = MAC (2 góc tương ứng)
mà 2 góc này ở vị trsi so le trong
=> BE // AC
b.
BE // AC (theo câu a)
=> AFD = BED (2 góc so le trong)
Xét tam giác DFA và tam giác DEB có:
AFD = BED (chứng minh trên)
DF = DE (gt)
FDA = EDB (2 góc đối đỉnh)
=> Tam giác DFA = Tam giác DEB (g.c.g)
=> FA = EB (2 cạnh tương ứng)
mà EB = AC (theo câu a)
=> FA = AC
=> A là trung điểm của FC
c.
Tam giác ABC có:
AB < AC (gt)
mà AC = EB (theo câu a)
=> AB < EB
=> BEM < BAM (quan hệ giữa góc và cạnh đối diện trong tam giác)
mà BEM = CAM (tam giác MBE = tam giác MCA)
=> CAM < BAM
Chúc bạn học tốt![]()
Phương An giúp mình làm bài hình còn lai được không?
đề nè
cho góc nhọn xOy; trên tia Ox lấy A(A#O); trên tia Oy lấy điểm B (B # O)sao cho OA = OB; kẻ ACvuông góc với OY (CE Oy) ; BD vuông góc Ox ( D E Ox); I là giao diểm của AC và BD
a. chứng minh tam giác AOC= tam giác BOD
b. So sánh IC và IA
c. Chứng minh tam giác AIB cân
d. Chứng minh góc IAB=M góc 1\2 góc AOB

a, Xét tam giác ACM và tam giác EMB có:
AM=ME
GÓC CMA =GÓC BME(đối đỉnh)
CM=MB
=> TAM GIÁC ACM=EMB( C.G.C)

đề bài phần a bị sai nhé bn , phải là BE // AC mới đúng
a ) Xét tam giác AMC và tam giác EMB có :
MA = ME ( gt )
\(\widehat{EMB}=\widehat{AMC}\) ( hai góc đối đỉnh )
MB = MC ( do AM là đường trung tuyến )
nên tam giác AMC = tam giác EMB ( c.g.c )
=> \(\widehat{CAM}=\widehat{MEB}\)
Mà hai góc này ở vị trí so le trong => BE//AC
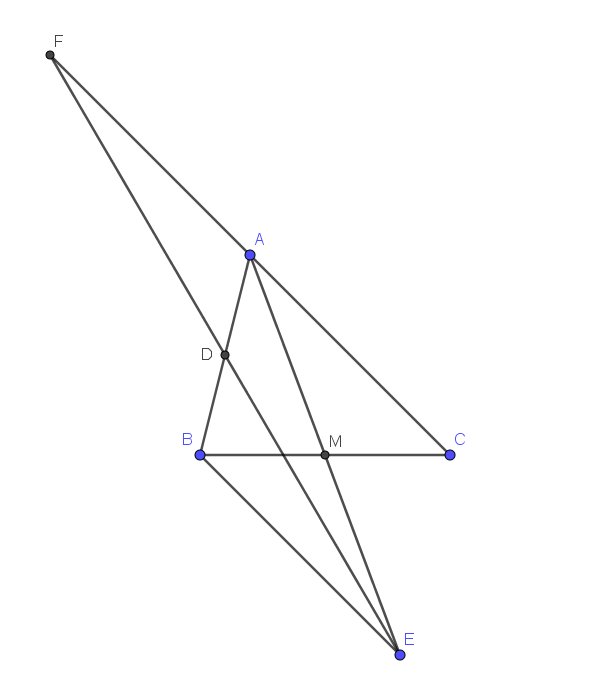
a) Xét \(\Delta AMC\)và \(\Delta EMB\)
+ AM = BM(gt)
+ MA = ME (gt)
+ Góc AMC = góc EMD (đối đỉnh)
Vậy hai tam giác trên bằng nhau theo trường hợp (c-g-c)
Ta có \(\widehat{EBM}=\widehat{ACM}\)(hai góc tương ứng)
Mà hai góc này nằm ở vị trí so le trong nên AC//BE
BE = AC (hai cạnh tương ứng)
b) Xét \(\Delta ADF\)và \(\Delta BDE\)
+ FD = DE(gt)
+ AD = BD (gt)
+ Góc ADF bằng góc BDE (đối đỉnh)
Vậy hai tam giác trên bằng nhau theo TH c.g.c
Ta suy ra được AF = BE
Và góc EBD = góc DAF (hai góc tương ứng)
Mà hai góc này nằm ở vị trí so le trong nên AF//BE
Lại có AF và AC cùng song song với BE nên A,F,C thẳng hàng(1)
BE = AC = AF (cmt) (2)
Từ (1) và (2) ta có A là trung điểm CF
Thank you