Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi K là hình chiếu vuông góc của E lên MD, suy ra góc MEK = 90 - BAC.
Ta có 2 tam giác đồng dạng EDK và MAE
suy ra MA/DE = ME/EK = 1/sin(A)
suy ra DE nhỏ nhất khi MA nhỏ nhất
suy ra M là chân đường cao hạ từ A

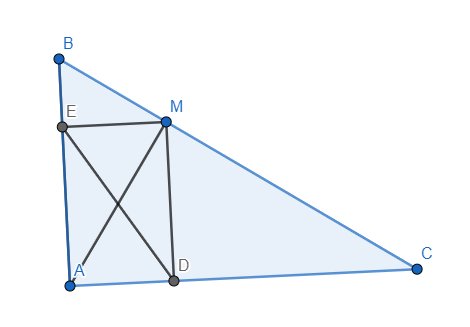
Do MD//AB và \(AB\perp AD\) nên \(MD\perp AD\) hay \(\widehat{ADM}=90^o\). Hoàn toàn tương tự, ta có \(\widehat{AEM}=90^o\). Mà \(\widehat{DAE}=90^o\) nên tứ giác ADME là hình chữ nhật. Do đó \(DE=AM\). Như vậy, ta quy về tìm vị trí của M trên BC để AM nhỏ nhất. Kẻ đường cao AH của tam giác ABC thì H cố định. Ta thấy AH và AM lần lượt là đường vuông góc và đường xiên kẻ từ A lên BC nên \(AM\ge AH\). Dấu "=" chỉ xảy ra khi \(M\equiv H\) hay M là chân đường vuông góc hạ từ A lên BC.
A C B K I
Để BI và CK nhỏ nhất :
\(\Leftrightarrow\) CM = MB
=> AM là trung tuyến của BC
=> M là trugn điểm của BC