Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét tam giác ABD và tam giác AED
AB=AE(Gt)
BAD=DAE(vì AD là tia p/giác)
AD là cạnh chung)
\(\Rightarrow\) tam giác ABD=tam giác AED(c.g.c)
b)Xét tam giác ADF và tam giác ADC
AF+AC(Gt)
BAD=DAE(vì AD là tia p/giác)
AD là cạnh chung
\(\Rightarrow\)tam giác ADF=tam giác ADC(c.g.c)
\(\Rightarrow\)DF=DC(cặp cạnh tương ứng)
c)Xét tam giác AMF và tam giác AMC
AF+AC(Gt)
BAD=DAE(vì AD là tia p/giác)
AD là cạnh chung
\(\Rightarrow\)tam giác AMF=tam giác AMC(c.g.c)
\(\Rightarrow\)AMF=AMC(cặp góc tương ứng)
Mà AMF+AMC=1800(kề bù)
\(\Rightarrow\)AMF=AMC=1800:2=900
Do đó Am vuông góc với CF
a)XÉT ▲ABD VÀ ▲AED CÓ:
AD CHUNG
AB=AE(GT)
GÓC BAD= GÓC EAD (AD LÀ PHÂN GIÁC)
=> ▲ABD= ▲AED(C-G-C)

a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
Suy ra: DB=DE
b: Xét ΔDBH và ΔDEC có
góc DBH=góc DEC
DB=DE
góc BDH=góc EDC
Do đó: ΔDBH=ΔDEC
c: Ta có: ΔDBH=ΔDEC
nên góc DHB=góc DCE
d: Ta có: AH=AB+BH
AC=AE+EC
mà AB=AE; BH=EC
nên AH=AC

1) Xét ΔCAB vuông tại A và ΔEAD vuông tại A có
AB=AD(gt)
AC=AE(gt)
Do đó: ΔCAB=ΔEAD(hai cạnh góc vuông)
Suy ra: BC=DE(hai cạnh tương ứng)
2) Xét ΔABD có AB=AD(gt)
nên ΔABD cân tại A(Định nghĩa tam giác cân)
Xét ΔABD cân tại A có \(\widehat{BAD}=90^0\)(gt)
nên ΔABD vuông cân tại A(Định nghĩa tam giác vuông cân)

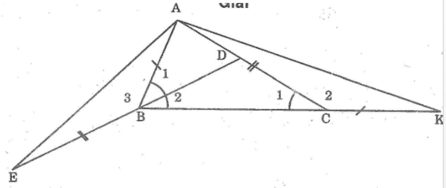
Vì BD là phân giác góc B=>ABD=1/2 góc B Vì B=2C=>ACB=1/2 góc B =>ABD=ACB Vì ABD và ABE là 2 góc kề bù=>.....+.....=180 độ Vì ACB và ACK là 2 góc kề bù=>.....+.....=180 độ =>ACK=ABE Xét tam giác ABE với tam giác ACK (c.g.c) =>AE=AK(đpcm)