D
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BC
1
BK
3 tháng 7 2021
Xét ▲ADC và ▲BCD có:
AD = BC ( gt )
AC = BD ( gt )
DC chung
=> ▲ADC = ▲BCD ( c.c.c )
=> góc D = góc C ( c.t.ứ )
cmtt ta đc góc A = Góc B
Mà Góc D + góc A + Góc C + Góc B=360o
=> 2GócA+2GócD=360o
-> gócA+gócD=180o ( 2 góc trong cùng phía )=>AB//DC -> ABCD là hình thang
Vì góc D = góc C (cmt) nên ABCD là hình thang cân
4 tháng 8 2015
Vì \(\Delta ABC\) cân tại B ( vì AB =BC)
=> Góc BAC = góc BCA (1)
Vì AC là phân giác góc A
=> góc BAC = góc CAD (2)
Từ (1) và (2) => góc BCA = góc CAD
Mà 2 góc này ở vị trí so le trong
=> AD // BC
=> ABCD là hình thang
Vậy ________________
S
4 tháng 7 2018
Tự vẽ hình
Tâ có: AB=BC (gt)
=> t/g ABC cân tại A
=> góc BAC = góc BCA
Mà góc BAC = góc CAD (AC là tia p/g của góc A)
=>góc CAD = góc BCA
Mà góc CAD và góc BCA là 2 góc ở vị trí so le trong
=> AB // CD
=> ABCD là hình thang
HH
7 tháng 7 2020
A B C D 1 2
Theo bài , ta có :
\(+AB=BC\Rightarrow\Delta ABC\)cân tại B
\(\Rightarrow\widehat{A_1}=\widehat{C_1}\left(1\right)\)
+ AC là tia phân giác góc A
\(\Rightarrow\widehat{A_2}=\widehat{A_1}\left(2\right)\)
Từ (1)(2) , suy ra : \(\widehat{A_2}=\widehat{C_1}\left(=\widehat{A_1}\right)\)
Mà hai góc này ở vị trí so le trong
=> AD // BC
Vậy ABCD là hình thang (đpcm)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 8 2020
Kéo dài AM cắt DC kéo dài tại E
+ Xét tg ABM và tg ECM có
^BAM = ^CEM (góc so le trong)
^AMB = ^CME (góc đối đỉnh)
=> tg ABM đồng dạng tg ECM \(\Rightarrow\frac{BM}{CM}=\frac{AM}{EM}=1\) => M là trung điểm của AE
=> AM là đường cao và đường trung tuyến của tg ADE => tg ADE cân tại D => DM là đường phân giác của ^ADC
NC
28 tháng 8 2020
A B M D C N
Bài làm:
Gọi N là trung điểm của AD
=> MN là đường trung bình của hình thang ABCD
=> MN // CD => \(\widehat{CDM}=\widehat{NMD}\) (so le trong) (1)
Lại có: MN là đường trung tuyến ứng với cạnh huyền của tam giác vuông AMD
=> \(MN=\frac{AD}{2}=ND\) => Tam giác MND cân tại N
=> \(\widehat{NMD}=\widehat{NDM}\) (2)
Từ (1) và (2) => \(\widehat{CDM}=\widehat{NDM}\)
=> DM là phân giác góc ADC
=> đpcm
21 tháng 4 2017
Bài giải:
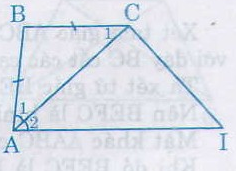
Ta có AB = BC (gt)
Suy ra ∆ABC cân
Nên ˆA1=ˆC1A1^=C1^ (1)
Lại có ˆA1=ˆA2A1^=A2^ (2) (vì AC là tia phân giác của ˆAA^)
Từ (1) và (2) suy ra ˆC1=ˆA2C1^=A2^
nên BC // AD (do ˆC1,ˆA2C1^,A2^ ở vị trí so le trong)
Vậy ABCD là hình thang
Q
21 tháng 4 2017
Ta có AB = BC (gt)
Suy ra: ∆ABC cân.
Nên \(\widehat{A_1}=\widehat{C_1}\) (1)
Lại có \(\widehat{A_1}=\widehat{A_2}\) (2) (vì AC là tia phân giác của ˆAA^)
Từ (1) và (2) suy ra \(\widehat{C_1}=\widehat{A_2}\)
nên BC // AD (do \(\widehat{A_1};\widehat{C_2}\) ở vị trí so le trong)
Vậy ABCD là hình thang.
2 tháng 2 2022
Bài 2:
a: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{CFE}=60^0\\\widehat{AEB}=\widehat{CEF}=60^0\end{matrix}\right.\)
=>ΔCFE đều
b: Xét tứ giác ABCD có
\(\widehat{BAC}=\widehat{BDC}=90^0\)
Do đó: ABCD là tứ giác nội tiếp