Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a) Ta có f'(x) = 3x2 + 1, g(x) = 6x + 1. Do đó
f'(x) > g'(x) <=> 3x2 + 1 > 6x + 1 <=> 3x2 - 6x >0
<=> 3x(x - 2) > 0 <=> x > 2 hoặc x > 0 <=> x ∈ (-∞;0) ∪ (2;+∞).
b) Ta có f'(x) = 6x2 - 2x, g'(x) = 3x2 + x. Do đó
f'(x) > g'(x) <=> 6x2 - 2x > 3x2 + x <=> 3x2 - 3x > 0
<=> 3x(x - 1) > 0 <=> x > 1 hoặc x < 0 <=> x ∈ (-∞;0) ∪ (1;+∞).

\(C'=0\) với mọi hằng số C
nguyen thi khanh nguyen
\(f'\left(x\right)=6x^2-2x\)
\(g'\left(x\right)=3x^2+x\)
\(f'\left(x\right)>g'\left(x\right)\Leftrightarrow6x^2-2x>3x^2+x\)
\(\Leftrightarrow3x^2-3x>0\Rightarrow\left[{}\begin{matrix}x>1\\x< 0\end{matrix}\right.\)

\(f'\left(x\right)=1-\dfrac{2x}{\sqrt{x^2+12}}\le0\\ \Leftrightarrow\sqrt{x^2+12}\le2x\\ \Leftrightarrow\left\{{}\begin{matrix}x^2+12\le4x^2\\x\ge0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x^2\ge12\\x\ge0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x^2\ge4\\x\ge0\end{matrix}\right.\Leftrightarrow x\ge2\)
Đáp số : \(\left[2,+\infty\right]\)
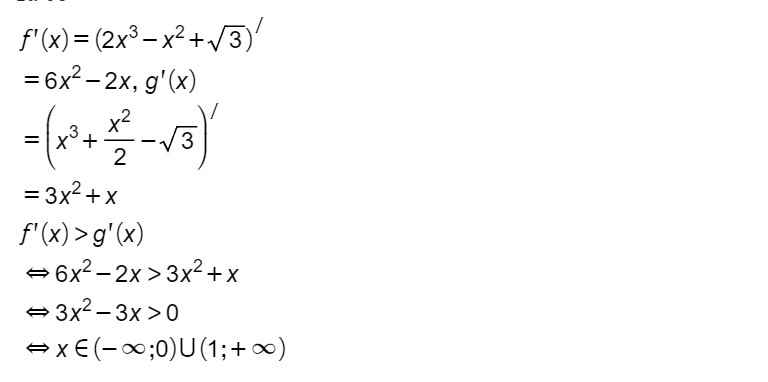
Tham khảo: