Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

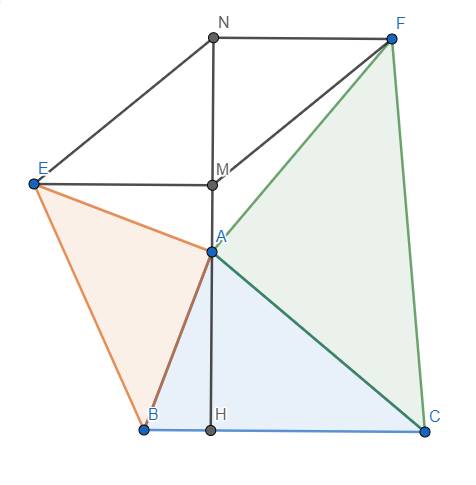
a) Do tam giác AEB vuông cân tại A nên \(\left\{{}\begin{matrix}\widehat{EAB}=90^o\\AE=AB\end{matrix}\right.\)
Ta thấy \(\widehat{MEA}=\widehat{BAH}\) vì chúng cùng phụ với \(\widehat{EAM}\)
Xét 2 tam giác HAB vuông tại H và MEA vuông tại M, ta có:
\(AE=AB\left(cmt\right),\widehat{MEA}=\widehat{BAH}\left(cmt\right)\)
\(\Rightarrow\Delta HAB=\Delta MEA\left(ch-gn\right)\) \(\Rightarrow AH=ME\) (1)
Tương tự, ta cũng có \(\Delta HAC=\Delta NFA\Rightarrow HC=AN\) (2)
Từ (1) và (2) suy ra \(EM+HC=AH+AN\) hay \(EM+HC=HN\) (đpcm)
b) Từ \(\Delta HAC=\Delta NFA\Rightarrow AH=NF\)
Từ đó suy ra \(ME=NF\left(=AH\right)\)
Xét tam giác MNE và NMF, ta có:
\(ME=NF\left(cmt\right),\widehat{EMN}=\widehat{FNM}\left(=90^o\right)\), MN là cạnh chung.
\(\Rightarrow\Delta MNE=\Delta NMF\left(c.g.c\right)\)
\(\Rightarrow\widehat{ENM}=\widehat{FMN}\) \(\Rightarrow\) EN//FM (2 góc so le trong bằng nhau)
Ta có đpcm.

a) Xét ∆AHB,∆EMA có :
^AHB = ^EMA = 90o
AB = AE (gt)
Do đó : ∆AHB = ∆EMA (ch-gn)
b) ∆AHB = ∆EMA (ch-gn)
=> EM = AH (1)
Cmtt ta cũng có : ∆AHC = ∆FNA (Ch-Gn)
=> HC = NA (2)
Từ (1)(2) => EM + HC = AH + NA
=> EM + HC = NH (A nằm giữa H,N)
d) Có : EM _|_ AH
FN _|_ AH
=> EM // FN

a.a. Ta có :
ΔAHB=ΔEMA(ch−gn)ΔAHB=ΔEMA(ch−gn)
AHBˆ=EMAˆ=(900)AHB^=EMA^=(900)
AB=AE(gt)AB=AE(gt)
ΔBAH=ΔAEMΔBAH=ΔAEM ( cùng phụ với ΔMAEΔMAE )
⇒EM=AH(1)⇒EM=AH(1)EM = AH (1)
Tương tự:
ΔAHC=ΔFNA(ch−gn)ΔAHC=ΔFNA(ch−gn)
⇒HC=NA(2)⇒HC=NA(2)
Từ (1)(1) và (2)(2) ⇒EM+HC=AH+NA=NH⇒EM+HC=AH+NA=NH
b) Từ ΔAHC=ΔFNAΔAHC=ΔFNA
⇒AH=NF(3)⇒AH=NF(3)
Từ (1)(1) và (3)(3)EM=MFEM=MF
Mặt khác : EM // NF ( cùng vuông góc với AH )
Ta suy ra : EN // FM

A B C E F M N
a) +)Xét tam giác EMA vuông tại M
=>góc MEA + góc MAE = 900(Định lí tổng 2 góc nhọn trong 1 tam giác vuông) (1)
+) Ta có: góc MAE + góc EAM + góc HAB = 1800
=> góc MAE + 900 + góc HAB = 1800
=>góc MAE + góc HAB = 1800(2)
Từ(1) và (2) => góc MEA= góc HAB (3)
+)Xét tam giác MEA và tam giác HAB có:
góc MEA = góc HAB(cm3)
AE=AB(vì tam giác ABE cân tại A)
góc EMA = góc AHB = 900
=>tam giác MEA= tam giác HAB(cạnh huyền-góc nhọn)
=> EM=AH(2 cạnh tương ứng) (4)
Tương tự chứng minh tam giác AHC= tam giác FNA(ch-gn)(6)
=>AN=HC(2 cạnh tương ứng) (5)
Từ (4) và (5) =>EM+HC=AN+AH
=>EM+HC=NH(đpcm)
b) +)Ta co: tam giác AHC=tam giác FNA (cm6)
=>AH=FN(2 cạnh tương ứng)(7)
từ (4) và (7)=>EM=FN(8)
+)Xét tam giác NEM và tam giác MFN có:
EM=FN(cm8)
góc EMN=góc FNM=900
MN là cạnh chung
=>tam giác NEM= tam giác MFN(cgc)
=>EN=FM(2 cạnh tương ứng)

Bài 1
\(3A=1.2.3+2.3.3+3.4.3+...+n\left(n+1\right)=\)
\(=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+n.\left(n+1\right)\left[\left(n+2\right)-\left(n-1\right)\right]=\)
\(=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-...-\left(n-1\right).n.\left(n+1\right)+n\left(n+1\right)\left(n+2\right)=\)
\(=n\left(n+1\right)\left(n+2\right)\Rightarrow A=\dfrac{n\left(n+1\right)\left(n+2\right)}{3}\)
Bài 2
B C A E F M N H
a/
Xét tg vuông AEM có
\(\widehat{EAM}+\widehat{AEM}=90^o\)
Ta có
\(\widehat{EAM}+\widehat{BAH}=\widehat{MAH}-\widehat{BAE}=180^o-90^o=90^o\)
\(\Rightarrow\widehat{AEM}=\widehat{BAH}\)
Xét tg vuông AEM và tg vuông BAH có
\(\widehat{AEM}=\widehat{BAH}\)
AE=AB (cạnh bên tg cân)
=> tg AEM = tg BAH (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
\(\Rightarrow EM=AH\) (1)
Xét tg vuông ANF có
\(\widehat{FAN}+\widehat{AFN}=90^o\)
Ta có
\(\widehat{FAN}+\widehat{CAH}=\widehat{NAH}-\widehat{FAC}=180^o-90^o=90^o\)
\(\Rightarrow\widehat{AFN}=\widehat{CAH}\)
Xét tg vuông AFN và tg vuông CAH có
\(\widehat{AFN}=\widehat{CAH}\)
AF=AC (cạnh bên tg cân)
=> tg AFN = tg CAH (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau) => HC=AN (2)
Từ (1) và (2) => EM+HC=AH+AN=NH
b/
Ta có
tg AFN = tg CAH (cmt) => FN=AH
Mà EM=AH (cmt)
=> EM=FN
\(EM\perp AH\left(gt\right);FN\perp AH\left(gt\right)\) => EM//FN (cùng vuông góc với AH)
=> ENFM là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
=> EN//FM (trong hbh (2 cạnh đối // với nhau)
B C A E F H M N
Xét ∆AHB,∆EMA có :
^AHB = ^EMA = 90o
AB = AE (gt)
^BAH = ^AEM (vì cùng phụ với ^MAE)
Do đó : ∆AHB = ∆EMA (Ch - Gn)
=> EM = AH (1)
Cmtt ta cũng có : ∆AHC = ∆FNA (Ch-Gn)
=> HC = NA (2)
Từ (1)(2) => EM + HC = AH + NA
=> EM + HC = NH (A nằm giữa H,N)
b) Có : EM _|_ AH
FN _|_ AH
=> EM // FN