Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
∆ABC vuông tại A, AH, vuông góc BC
=> AB.AH = HB.AC
=> AB = 15Ta có: BC^2 = AB^2 + AC^2=> BC = 25=> HB = BC - BH = 25-9 = 16
a) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AH^2+BH^2=AB^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Vậy: AB=15cm

a ) Ta có : AB² + AC² = 8² + 6² = 100
BC² = 10² = 100
=> AB² + AC² = BC²
=> Tam giác ABC vuông tại A ( Định lý Py-ta-go đảo )
b ) Áp dụng định lý Py - ta - go vào ΔABH vuông tại H có :
AH² + BH² = AB²
Hay AH² + 6,4² = 8²
<=> AH² = 64 - 40,96 = 23,04
=> AH = 4,8 cm

A B H C 4,5 8 6
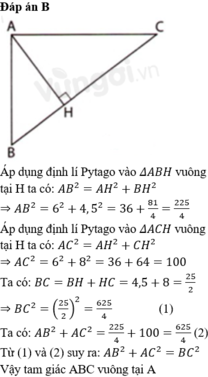
Xét \(\Delta AHB\) vuông tại H có :
\(AB^2=AH^2+BH^2\) (Định lí PYTAGO)
=> \(AB^2=6^2+4,5^2\)
=> \(AB^2=56,25\)
=> \(AB=\sqrt{56,25}=7,5\) (cm)
Xét \(\Delta AHC\perp H\) có :
\(AC^2=AH^2+HC^2\) (Định lí PYTAGO)
=> \(AC^2=6^2+8^2\)
=> \(AC^2=100\)
=> \(AC=\sqrt{100}=10\left(cm\right)\)
Áp dụng định lí PYTAGO đảo vào \(\Delta ABC\) , ta có :
\(AB^2+AC^2=BC^2\)
=> \(7,5^2+10^2=156,25\)
=> \(BC^2=12,5\)
Vậy tam giác ABC là tam giác vuông (đpcm)

a) Xét tam giác BAH và tam giác CAH, có:
AH: cạnh chung
AB = AC ( tam giác ABC cân tại A )
góc AHB = góc AHC ( = 90 độ )
-> tam giác BAH = tam giác CAH ( ch-cgv )
-> HB = HC ( 2 cạnh tương ứng )
b) Xét tam giác FBH và tam giác ECH, có:
HB = HC ( cmt )
góc D = góc E ( = 90 độ )
góc B = góc C ( tam giác ABC cân tại A )
-> tam giác FBH = tam giác ECH ( ch-gn )
-> HF = HE ( 2 cạnh tương ứng )
-> tam giác HEF là tam giác cân tại H
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
b) Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
BH=CH(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔFHB=ΔEHC(cạnh huyền-góc nhọn)
Suy ra: HF=HE(Hai cạnh tương ứng)
Xét ΔHEF có HF=HE(cmt)
nên ΔHEF cân tại H(Định nghĩa tam giác cân)