Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu 1:
Gọi \(A\left(1;-1\right)\) và \(B\left(2;3\right)\Rightarrow\) tập hợp \(z\) thoả mãn điều kiện đề bài là đường trung trực d của đoạn AB, ta dễ dàng viết được phương trình d có dạng \(4x-y-5=0\)
Gọi \(M\left(-2;-1\right)\) và \(N\left(3;-2\right)\) và \(I\left(a;b\right)\) là điểm bất kì biểu diễn \(z\Rightarrow I\in d\) \(\Rightarrow P=IM+IN\). Bài toán trở thành dạng cực trị hình học phẳng quen thuộc: cho đường thẳng d và 2 điểm M, N cố định, tìm I thuộc d để \(P=IM+IN\) đạt GTNN
Thay toạ độ M, N vào pt d ta được 2 giá trị trái dấu \(\Rightarrow M;N\) nằm về 2 phía so với d
Gọi \(C\) là điểm đối xứng M qua d \(\Rightarrow IM+IN=IC+IN\), mà \(IC+IN\ge CN\Rightarrow P_{min}=CN\) khi I, C, N thẳng hàng
Phương trình đường thẳng d' qua M và vuông góc d có dạng:
\(1\left(x+2\right)+4\left(y+1\right)=0\Leftrightarrow x+4y+6=0\)
Gọi D là giao điểm d và d' \(\Rightarrow\left\{{}\begin{matrix}x+4y+6=0\\4x-y-5=0\end{matrix}\right.\) \(\Rightarrow D\left(\frac{14}{17};-\frac{29}{17}\right)\)
\(\overrightarrow{MD}=\overrightarrow{DC}\Rightarrow C\left(-2;-1\right)\Rightarrow P_{min}=CN=\sqrt{\left(3+2\right)^2+\left(-2+1\right)^2}=\sqrt{26}\)
Bài 2:
Tập hợp \(z\) là các điểm M thuộc đường tròn (C) tâm \(I\left(0;1\right)\) bán kính \(R=\sqrt{2}\) có phương trình \(x^2+\left(y-1\right)^2=2\)
\(\Rightarrow\left|z\right|=OM\Rightarrow\left|z\right|_{max}\) khi và chỉ khi \(M;I;O\) thẳng hàng và M, O nằm về hai phía so với I
\(\Rightarrow M\) là giao điểm của (C) với Oy \(\Rightarrow M\left(0;1+\sqrt{2}\right)\Rightarrow\) phần ảo của z là \(b=1+\sqrt{2}\)
Câu 3:
\(\overline{z}=\left(i+\sqrt{2}\right)^2\left(1-\sqrt{2}i\right)=5+\sqrt{2}i\)
\(\Rightarrow z=5-\sqrt{2}i\Rightarrow b=-\sqrt{2}\)
Câu 4
\(z.z'=\left(m+3i\right)\left(2-\left(m+1\right)i\right)=2m-\left(m^2+m\right)i+6i+3m+3\)
\(=5m+3-\left(m^2+m-6\right)i\)
Để \(z.z'\) là số thực \(\Leftrightarrow m^2+m-6=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-3\end{matrix}\right.\)
Câu 5:
\(A\left(-4;0\right);B\left(0;4\right);M\left(x;3\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(4;4\right)\\\overrightarrow{AM}=\left(x+4;3\right)\end{matrix}\right.\) \(\Rightarrow A,B,M\) khi và chỉ khi \(\frac{x+4}{4}=\frac{3}{4}\Rightarrow x=-1\)
Câu 6:
\(z=3z_1-2z_2=3\left(1+2i\right)-2\left(2-3i\right)=-1+12i\)
\(\Rightarrow b=12\)
Câu 7:
\(w=\left(1-i\right)^2z\)
Lấy môđun 2 vế:
\(\left|w\right|=\left|\left(1-i\right)^2\right|.\left|z\right|=2m\)
Câu 8:
\(3=\left|z-1+3i\right|=\left|z-1-i+4i\right|\ge\left|\left|z-1-i\right|-\left|4i\right|\right|=\left|\left|z-1-i\right|-4\right|\)
\(\Rightarrow\left|z-1-i\right|\ge-3+4=1\)
Đáp án B.
Đặt 
suy ra tập hợp các điểm M(z) = (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R =
5
Ta có 
Ta cần tìm P sao cho đường thẳng ∆ và đường tròn (C) có điểm chung
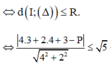
Do đó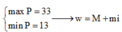 
Đáp án B
Đặt 
suy ra tập hợp các điểm M(z)= (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R=
5
.
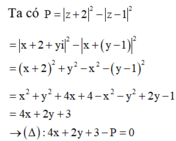
Ta cần tìm P sao cho đường thẳng ∆ và đường tròn (C) có điểm chung
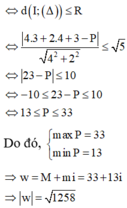
Lời giải:
Đặt \(z=a+bi\). Ta có: \(|z|\leq 2\Leftrightarrow a^2+b^2\leq 4\)
Có:
\(p=2|z+1|+2|z-1|+|z-\overline{z}-4i|\)
\(=2|(a+1)+bi|+2|(a-1)+bi|+|(a+bi)-(a-bi)-4i|\)
\(=2\sqrt{(a+1)^2+b^2}+2\sqrt{(a-1)^2+b^2}+\sqrt{(2b-4)^2}\)
\(=2\sqrt{(a+1)^2+b^2}+\sqrt{(a-1)^2+b^2}+4-2b\)
(do \(a^2+b^2\leq 4\Rightarrow b^2\leq 4\Rightarrow b\leq 2\Rightarrow \sqrt{(2b-4)^2}=4-2b\) )
\(\Leftrightarrow p=2[\sqrt{(a+1)^2+b^2}+\sqrt{(a-1)^2+b^2}-b+2]\)
Theo BĐT Mincopxky :
\(p\geq 2(\sqrt{(a+1+1-a)^2+(b+b)^2}-b+2)\)
\(\Leftrightarrow p\geq 2(2\sqrt{b^2+1}-b+2)\)
Xét \(f(b)=2\sqrt{b^2+1}-b+2\) với \(b\in [-2;2]\)
Có: \(f'(b)=\frac{2b}{\sqrt{b^2+1}}-1=0\Leftrightarrow b=\pm \frac{\sqrt{3}}{3}\)
Lập bảng biến thiên ta suy ra \(f(b)_{\min}=f(\frac{\sqrt{3}}{3})=2+\sqrt{3}\)
\(\Rightarrow p\geq 2f(b)\geq 2(2+\sqrt{3})\)
Vậy \(p_{\min}=4+2\sqrt{3}\)
Dấu bằng xảy ra khi \(b=\frac{\sqrt{3}}{3}; \frac{a+1}{1-a}=\frac{b}{b}=1\Rightarrow a=0\)
Đặt \(z=x+yi\)
\(\left|x+yi+x-yi+2\right|+2\left|x+yi-x+yi-2i\right|\le12\)
\(\Leftrightarrow\left|2x+2\right|+4\left|\left(y-1\right)i\right|\le12\)
\(\Leftrightarrow\left|x+1\right|+2\left|y-1\right|\le6\)
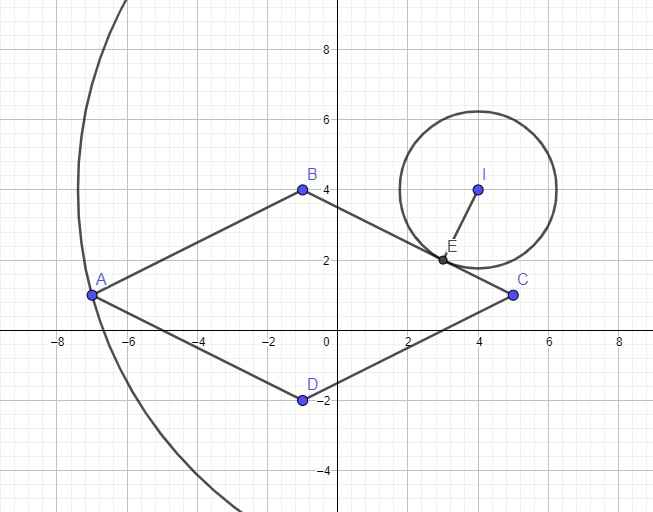
Tập hợp z là miền trong hình thoi (gồm cả biên) với 4 đỉnh: \(A\left(-7;1\right)\) ; \(B\left(-1;4\right)\) ; \(C\left(5;1\right)\) ; \(D\left(-1;-2\right)\)
\(P^2=\left|z-4-4i\right|^2=\left(x-4\right)^2+\left(y-4\right)^2\) có tập hợp là đường tròn (C) tâm \(I\left(4;4\right)\) bán kính \(R=P>0\) sao cho (C) và hình thoi ABCD có ít nhất 1 điểm chung
Từ hình vẽ ta thấy \(P_{max}\) khi (C) đi qua A \(\Rightarrow P=IA\) và \(P_{min}\) khi (C) tiếp xúc BC \(\Rightarrow P=d\left(I;BC\right)\)
\(\overrightarrow{IA}=\left(-11;-3\right)\Rightarrow M=IA=\sqrt{130}\)
\(\overrightarrow{BC}=\left(6;-3\right)\Rightarrow\) đường thẳng BC nhận (1;2) là 1 vtpt
Phương trình BC: \(1\left(x+1\right)+2\left(y-4\right)=0\Leftrightarrow x+2y-7=0\)
\(\Rightarrow m=d\left(I;BC\right)=\dfrac{\left|4+2.4-7\right|}{\sqrt{1^2+2^2}}=\sqrt{5}\)
\(\Rightarrow M+m=\sqrt{130}+\sqrt{5}\)
đặc \(z=a+bi\) với \(\left(a;b\in R;i^2=-1\right)\)
ta có : \(\left|z-\overline{z}+2i\right|=\left|\dfrac{3}{2}z+\dfrac{1}{2}\overline{z}\right|\)
\(\Leftrightarrow\left|a+bi-a+bi+2i\right|=\left|\dfrac{3}{2}a+\dfrac{3}{2}bi+\dfrac{1}{2}a-\dfrac{1}{2}bi\right|\)
\(\Leftrightarrow\sqrt{\left(2b+2\right)^2}=\sqrt{\left(2a+b\right)^2}\) \(\Leftrightarrow2b+2=2a+b\Leftrightarrow a=\dfrac{b}{2}+1\)
ta có : \(P=\left|z-3\right|=\left|a+bi-3\right|=\sqrt{\left(a-3\right)^2+b^2}\)
\(\Leftrightarrow P=\sqrt{\left(\dfrac{b}{2}+1-3\right)^2+b^2}=\sqrt{\left(\dfrac{b}{2}-2\right)^2+b^2}\)
\(\Leftrightarrow P=\sqrt{\dfrac{5b^2}{4}-2b+4}\ge\sqrt{4-\dfrac{\left(-2\right)^2}{4.\dfrac{5}{4}}}=\dfrac{4\sqrt{5}}{5}\)
dấu "=" xảy ra khi \(b=\dfrac{2}{2.\dfrac{5}{4}}=\dfrac{4}{5}\) và \(a=\dfrac{7}{5}\) \(\Leftrightarrow z=\dfrac{7}{5}+\dfrac{4}{5}i\)
Lời giải:
Ta có:
\(|z^2+1|=4|z|\Leftrightarrow \frac{|z^2+1|^2}{|z|^2}=16\)
\(\Leftrightarrow 16=\frac{(z^2+1)(\overline{z^2}+1)}{|z|^2}=\frac{|z|^4+z^2+\overline{z^2}+1}{|z|^2}\)
\(\Leftrightarrow 16=\frac{|z|^4+(z+\overline{z})^2-2|z|^2+1}{|z|^2}\geq \frac{|z|^4-2|z|^2+1}{|z|^2}\)
Đặt \(|z|^2=t\Rightarrow 16\geq \frac{t^2-2t+1}{t}\)
\(\Leftrightarrow t^2-18t+1\leq 0\Leftrightarrow 9-4\sqrt{5}\leq t\leq 9+4\sqrt{5}\)
\(\Rightarrow \sqrt{5}-2\leq |z|\leq \sqrt{5}+2\) hay \(|z|_{\min}=\sqrt{5}-2;|z|_{\max}=\sqrt{5}+2\)
Tổng quát: Nếu \(|z+\frac{1}{z}|=k\Rightarrow |z|_{\max}=\frac{\sqrt{k^2+4}+k}{2};|z|_{\min}=\frac{\sqrt{k^2+4}-k}{2}\)
Mọi điểm M biểu diễn z đều phải thỏa mãn 2 điều kiện: vừa thuộc đường tròn (C) vừa thuộc đường thẳng \(\Delta\) (tham số P)
Do đó, M là giao điểm của (C) và \(\Delta\)
Hay tham số P phải thỏa mãn sao cho (C) và \(\Delta\) có ít nhất 1 điểm chung
Hay hệ pt nói trên có nghiệm (thật ra chi tiết đó là thừa, chỉ cần biện luận (C) và \(\Delta\) có ít nhất 1 điểm chung \(\Rightarrow d\left(I;\Delta\right)\le R\) là đủ)
từ chỗ \(\left(\Delta\right)\) con có được suy ra tập hợp \(z\) là một đường thẳng \(y=-2x+\dfrac{P-3}{2}\) không ạ?