Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Khim=0 thì (1) trở thành \(x^2-2=0\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
Khi m=1 thì (1) trở thành \(x^2-2x=0\)
=>x=0 hoặc x=2
b: \(\text{Δ}=\left(-2m\right)^2-4\left(2m-2\right)\)
\(=4m^2-8m+8=4\left(m-1\right)^2>=0\)
Do đó: Phương trình luôn có hai nghiệm

\(\left(m+1\right)x^2-2\left(m-1\right)x+m-3=0\) (1)
a) Phương trình (1) có 2 nghiệm phân biệt khi và chỉ khi:
\(\Delta'=\left(m-1\right)^2-\left(m+1\right)\left(m-3\right)>0\)
\(\Leftrightarrow\left(m^2-2m+1\right)-\left(m^2-2m-3\right)>0\)
\(\Leftrightarrow4>0\)(luôn đúng)
Vậy phương trình có 2 nghiệm phân biệt với mọi m.
b) Để t nghĩ tí

\(a,\Delta=m^2-4m+4=\left(m-2\right)^2\ge0\forall m\)
Nên pt đã cho luôn có 2 nghiệm phân biệt với mọi m
b, Theo Vi-ét \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}}\)
Ta có \(B=\frac{2x_1x_2+3}{x_1^2+x_2^2+2\left(1+x_1x_2\right)}=1\)
\(\Leftrightarrow\frac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=1\)
\(\Leftrightarrow\frac{2\left(m-1\right)+3}{m^2+2}=1\)
\(\Leftrightarrow\frac{2m+1}{m^2+2}=1\)
\(\Leftrightarrow2m+1=m^2+2\)
\(\Leftrightarrow m^2-2m+1=0\)
\(\Leftrightarrow\left(m-1\right)^2=0\)
\(\Leftrightarrow m=1\)

câu a bạn áp dụng hệ thức Viet rồi rút m và thay vào cái kia r tìm ra thôi
![]()

a, Khi m = 0 thì :
pt <=> x^2+2x-3 = 0
<=> (x-1).(x+3) = 0
<=> x-1=0 hoặc x+3=0
<=> x=1 hoặc x=-3
Tk mk nha

\(a)\) Ta có : \(\Delta=\left(-m\right)^2-4\left(m-3\right)=m^2-4m+12=\left(m^2-4m+4\right)+8=\left(m-2\right)^2+8>0\)
Vậy pt (1) có hai nghiệm phân biệt với mọi m
\(b)\) Có \(x_1^2+x_2^2=5\)\(\Leftrightarrow\)\(\left(x_1+x_2\right)^2-2x_1x_2=5\) (*)
Theo định lý Vi-et ta có : \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-3\end{cases}}\)
(*) \(\Leftrightarrow\)\(m^2-2\left(m-3\right)=5\)
\(\Leftrightarrow\)\(m^2-2m+1=0\)
\(\Leftrightarrow\)\(m=1\)
Vậy để \(x_1^2+x_2^2=5\) thì \(m=1\)
\(c)\)......... -_-
Theo hệ thức Vi et( ý b) \(\hept{\begin{cases}X_1+X_2=m\\X_1.X_2=m-3\end{cases}\Rightarrow}X_1.X_2=X_1+X_2-3\)(thế \(X_1+X_2=m\)vô phương trình dưới)
Vậy hệ thức liên hệ giữa X1 X2 không chứa m là \(X_1X_2=X_1 +X_2-3\)
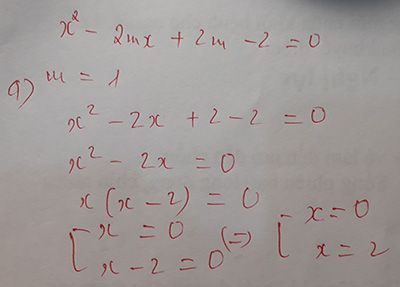
=> x2 = m2 + 2m + 1 = (m+1)2 => x1 = m + 1; x2 = -(m+1)
=> x1 + x2 = 0