Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,
\(x^2+y^2=\left(x+y\right)^2-2xy=1^2-2\cdot\left(-6\right)=1-\left(-12\right)=13\)
\(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=1\cdot\left[13-\left(-6\right)\right]=19\)
\(x^5+y^5=\left(x+y\right)\left(x^2+y^2\right)^2-\left(2x^3y^2+xy^4+x^4y+2x^2y^3\right)=169-\left[2\left(xy\right)^2\left(x+y\right)+xy\left(x^3+y^3\right)\right]=169-\left[2\cdot36\cdot1-6\cdot19\right]=211\)

a) Ta có:
x + y = 3
=> ( x + y)2 = 9
=> x2 + 2xy + y2 = 9
=> 10 + 2xy = 9
=> 2xy = 9 - 10 = -1
=> xy = -1/2
Ta có:
x3 + y3 = (x + y)(x2 - xy + y2)
= 3.(10 + 1/2) = 63/2
b) Ta có: x + y = a
=> (x + y)2 = a2
=> x2 + 2xy + y2 = a2
=> b + 2xy = a2
=> xy = (a2 - b)/2
Ta có: x3 + y3 = (x + y)(x2 + xy + y2)
= a[b + (a2 - b )/2] = ab + (a3 - b)/2.
Làm b) công thức tổng quát luôn
x+y=a => (x+y)^2 =a^2 => x^2+y^2+2xy=a^2
Thay x^2+y^2=b vào ta được:
b+2xy=a^2 => xy=(a^2-b)/2
TA có x^3+y^3 =(x+y)(x^2+y^2 -xy)= a [b+(a^2-b)/2] =ab +(a^3-ab)/2=ab/2+a^3/2

x - 4 = 2 => x = 2 + 4 => x = 6
x + y = 4 mà x = 6 => y = 4 - 6 => y = -2
=> xy = 6 \(\times\) (-2) = -12
x3 - y3 = 63 - (-2)3 = 224
Ta có:\(x-4=2\Rightarrow x=6^{\left(1\right)}\)
Thay \(^{\left(1\right)}\) vào \(x+y=4\) ,ta được:
\(6+y=4\Rightarrow y=-2^{\left(2\right)}\)
Thay \(^{\left(1\right),\left(2\right)}\) vào xy ,ta được:
\(xy=6.\left(-2\right)=-12\)
thay \(^{\left(1\right),\left(2\right)}\) vào \(x^3-y^3\), ta được:
\(x^3-y^3=6^3-\left(-2\right)^3=216-\left(-8\right)=216+8=224\)

b: \(=3\left[\left(x+y\right)^2-2xy\right]-2\left[\left(x-y\right)^3+3xy\left(x-y\right)\right]\)
\(=3\left(1-2xy\right)-2\left(1+3xy\right)\)
\(=3-6xy-2-6xy=-12xy+1\)
c: \(=\left(x+y\right)^3-3\left(x^2+y^2+2xy\right)+3\left(x+y\right)+2012\)
\(=101^2-3\cdot101^2+3\cdot101+2012\)
=1002013

a) B= 2x2-3x+1
=(2x2-2x)-(x-1)
=2x(x-1)-(x-1)
=(2x-1)(x-1)
\(\left|x\right|=\frac{1}{2}\)nên ta có \(x=\frac{1}{2}\)hoặc\(x=\frac{-1}{2}\)
nếu \(x=\frac{1}{2}\)thì
B=(2*\(\frac{1}{2}\)-1)(\(\frac{1}{2}\)-1)
B=0
nếu x= -1/2
thì B= (2*(-1/2)-1)(-1/2-1)
B=(-2)*(-3/2)
B=3

theo đầu bài ta có\(\dfrac{x^2+y^2}{xy}=\dfrac{10}{3}\)=>\(3x^2+3y^2=10xy\)
A=\(\dfrac{x-y}{x+y}\)
=>\(A^2=\left(\dfrac{x-y}{x+y}\right)^2=\dfrac{x^2-2xy+y^2}{x^2+2xy+y^2}=\dfrac{3x^2-6xy+3y^2}{3x^2+6xy+3y^2}=\dfrac{10xy-6xy}{10xy+6xy}=\dfrac{4xy}{16xy}=\dfrac{1}{4}\)
=>A=\(\sqrt{\dfrac{1}{4}}=\dfrac{-1}{2}hoặc\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\) (cộng trừ căn 1/4 nhé)
vì y>x>0=> A=-1/2

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
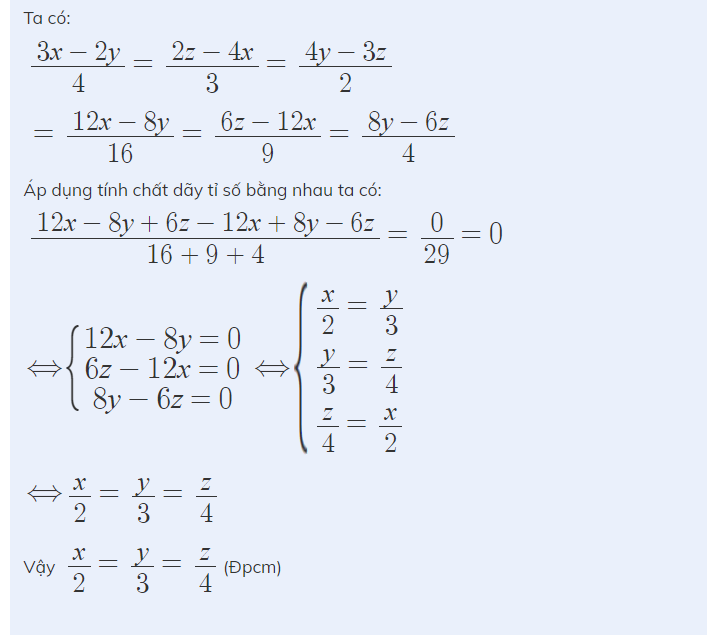

ĐÂY NÀY:
( x +y) ^2 = a^2 => x^2 + 2xy + y^2 = a^2
=> 2xy = a^2 - ( x^2 + y^2) = a^2 -b
=> xy = a^2-b/2
Ta có E = x^3 + y^3 = ( x+ y)( x^2 - xy + y^2)
E = a ( b - a^2-b/2)

a. \(=x^3+2^3+1^3-x^3\)
\(=\left(x^3-x^3\right)+8+1\)
\(=0+8+1\)
\(=9\)
Bài 1 :
a) ( x + 2 )( x2 - 2x + 4 ) + (1 - x)(1+x+ + x2 )
= ( x3 - 8 ) + ( 1 - x3 )
= x3 - 8 + 1 - x3
= 7
b) 7x( 4x - 2) - ( x - 3)( x+1 ) + 16x
= 28x2 - 14x - x2 - x + 3x + 3 + 16x
= 27x2 + 3
b)
Gửi câu trả lời c
a)x^2+y^2=5
<=> (x+y)^2- 2xy = 5
<=> 9-2xy=5
suy ra xy=2
mà x+y=3
Do đó x=1, y=2 hoặc x=2, y=1
Vậy x^3+y^3=1^3+2^3=2^3+1^3=9