Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để phương trình có hai nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}\Delta\ge0\\a\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(3m-1\right)^2-4.\left(m+1\right)\left(2m-2\right)\ge0\\\Delta\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+9\ge0\\m\ne-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-3\right)^2\ge0\\m\ne1\end{matrix}\right.\)\(\Leftrightarrow m\ne1\).
Áp dụng định ly Viet:
\(x_1+x_2=-\dfrac{3m-1}{m+1}=3\)\(\Leftrightarrow3m-1=-3m-3\)\(\Leftrightarrow6m=-2\)\(\Leftrightarrow m=-\dfrac{1}{3}\).
Vậy \(m=-\dfrac{1}{3}\) là giá trị cần tìm.

\(\Delta=\left(2m+1\right)^2-4\left(m^2+m-2\right)=9>0\)
\(\Rightarrow\) phương trình luôn có 2 nghiệm phân biệt: \(\left\{{}\begin{matrix}x_1=\frac{2m+1+3}{2}=m+2\\x_2=\frac{2m+1-3}{2}=m-1\end{matrix}\right.\)
Để phương trình có 2 nghiệm âm phân biệt:
\(\Rightarrow x_1< 0\Rightarrow m+2< 0\Rightarrow m< -2\)
Khi đó:
\(A=x_1\left(x_2+5\right)=\left(m+2\right)\left(m-1+5\right)=\left(m+2\right)\left(m+4\right)\)
\(A=m^2+6m+8=\left(m+3\right)^2-1\ge-1\)
\(\Rightarrow A_{min}=-1\) khi \(m+3=0\Leftrightarrow m=-3< -2\) (thỏa mãn)

\(\Delta=\left(2m-2\right)^2-4\cdot2\cdot\left(m^2-1\right)\)
\(=4m^2-8m+4-8m^2+8\)
\(=-4m^2-8m+12\)
Để phương trình có hai nghiệm phân biệt thì -4m^2-8m+12>0
=>4m^2+8m-12<0
=>m^2+2m-3<0
=>(m+3)(m-1)<0
=>-3<m<1
\(A=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=\left(\dfrac{2m-2}{2}\right)^2-4\cdot\dfrac{m^2-1}{2}\)
\(=\left(m-1\right)^2-2\left(m^2-1\right)\)
\(=m^2-2m+1-2m^2+2=-m^2-2m+3\)
\(=-\left(m^2+2m-3\right)\)
\(=-\left(m^2+2m+1-4\right)\)
\(=-\left(m+1\right)^2+4< =4\)
Dấu = xảy ra khi m=-1

Để phương trình có hai nghiệm phân biệt âm :
\(\left\{{}\begin{matrix}\Delta>0\\S< 0\\P>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m^2-1\right)^2-9>0\left(1\right)\\\dfrac{-2\left(m^2-1\right)}{9.2}< 0\left(2\right)\\\dfrac{1}{9}>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(m^2-1\right)^2>9\\m^2-1>0\end{matrix}\right.\)
Với \(m>2\) thì \(\left(m^2-1\right)^2-9>\left(2^2-1\right)^2-9=0\) nên (1) thỏa mãn.
Với \(m>2\) thì \(m^2-1>2^2-1=3>0\) nên (2) thỏa mãn.
Vậy \(m>2\) phương trình có hai nghiệm âm.
Để phương trình có hai nghiệm thì:
\(\left\{{}\begin{matrix}a\ne0\\\Delta\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(m^2-1\right)^2-9\ge0\\9\ne0\end{matrix}\right.\)
Áp dụng định lý Viet ta được:
\(x_1+x_2=\dfrac{-2\left(m^2-1\right)}{9}=4\) \(\Leftrightarrow m^2-1=-18\)
\(\Leftrightarrow m^2=-17\) (loại)
Vậy không có giá trị m thỏa mãn.
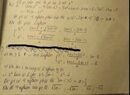

\(\Delta=\left(3m+2\right)^2-12m=9m^2+4>0\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3m-2\\x_1x_2=3m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+1+x_2+1=-3m\\x_1x_2+x_1+x_2+1=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+1+x_2+1=-3m\\\left(x_1+1\right)\left(x_2+1\right)=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}x_1+1=a\\x_2+1=b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a+b=-3m\\ab=-1\end{matrix}\right.\)
\(Q=a^4+b^4\ge2a^2b^2=2\)
Dấu "=" xảy ra khi \(a^2=b^2\Rightarrow\left[{}\begin{matrix}a=b\left(loại\right)\\a=-b\end{matrix}\right.\)
\(\Rightarrow-3m=0\Rightarrow m=0\)