Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\Delta=m^2-4m+4=\left(m-2\right)^2\ge0\forall m\)
Nên pt đã cho luôn có 2 nghiệm phân biệt với mọi m
b, Theo Vi-ét \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}}\)
Ta có \(B=\frac{2x_1x_2+3}{x_1^2+x_2^2+2\left(1+x_1x_2\right)}=1\)
\(\Leftrightarrow\frac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=1\)
\(\Leftrightarrow\frac{2\left(m-1\right)+3}{m^2+2}=1\)
\(\Leftrightarrow\frac{2m+1}{m^2+2}=1\)
\(\Leftrightarrow2m+1=m^2+2\)
\(\Leftrightarrow m^2-2m+1=0\)
\(\Leftrightarrow\left(m-1\right)^2=0\)
\(\Leftrightarrow m=1\)

Trả lời
a) Delta phương trình đó rồi xét 2 trường hợp
b) phần à delta lên sẽ tìm được m rồi thế vào là xong
Chắc vậy không chắc cho nắm

\(a)\) Để pt có hai nghiệm phân biệt \(x_1,x_2\) thì \(\Delta'=\left(1-m\right)^2-m^2+3m=1-2m+m^2-m^2+3m=m+1>0\)\(\Leftrightarrow\)\(m>-1\)
Vậy để pt có hai nghiệm phân biệt \(x_1,x_2\) thì \(m>-1\)
\(b)\) Ta có : \(T=x_1^2+x_2^2-\left(m-1\right)\left(x_1+x_2\right)+m^2-3m\)
\(T=\left(x_1+x_2\right)^2-2x_1x_2+\left(1-m\right)\left(x_1+x_2\right)+m^2-3m\)
Theo định lý Vi-et ta có : \(\hept{\begin{cases}x_1+x_2=2\left(1-m\right)\\x_1x_2=m^2-3m\end{cases}}\)
\(\Rightarrow\)\(T=4\left(1-m\right)^2-2\left(m^2-3m\right)-2\left(1-m\right)\left(1-m\right)+m^2-3m\)
\(T=4m^2-8m+4-2m^2+6m-2m^2+4m-2+m^2-3m\)
\(T=m^2-m+2=\left(m^2-m+\frac{1}{4}\right)+\frac{7}{4}=\left(m-\frac{1}{2}\right)^2+\frac{7}{4}\ge\frac{7}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(m=\frac{1}{2}\) ( thoả mãn )
Vậy GTNN của \(T=\frac{7}{4}\) khi \(m=\frac{1}{2}\)

\(x^2-4x-m^2=0\) (1)
\(a)\) Để pt (1) có hai nghiệm phân biệt \(x_1,x_2\) thì \(\Delta'=\left(-2\right)^2-\left(-m\right)^2=4+m^2>0\) ( luôn đúng )
Vậy pt (1) luôn có hai nghiệm phân biệt \(x_1,x_2\) với mọi m
\(b)\) Ta có : \(A=\left|x_1^2-x_2^2\right|=\left|\left(x_1+x_2\right)\left(x_1-x_2\right)\right|\)
\(\Leftrightarrow\)\(A^2=\left(x_1+x_2\right)^2\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2\left(x_1^2+x_2^2-2x_1x_2\right)=\left(x_1+x_2\right)^2\left[\left(x_1+x_2\right)^2-4x_1x_2\right]\) (*)
Theo định lý Vi-et ta có : \(\hept{\begin{cases}x_1+x_2=4\\x_1x_2=-m^2\end{cases}}\)
(*) \(\Leftrightarrow\)\(A^2=4^2\left[4^2-4\left(-m^2\right)\right]=16\left(16+4m^2\right)=64m^2+256\ge256\)
\(\Leftrightarrow\)\(A\ge\sqrt{256}=16\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(64m^2=0\)\(\Leftrightarrow\)\(m=0\)
Vậy GTNN của \(A=16\) khi \(m=0\)
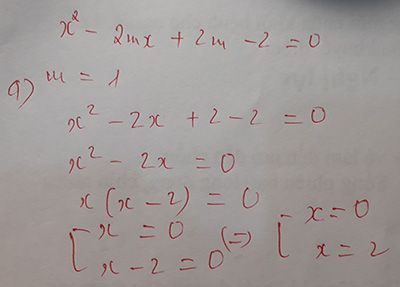
\(\Delta=m^2-4m+4=\left(m-2\right)^2\ge0\)
\(\Rightarrow\) pt đã cho luôn có 2 nghiệm
Theo Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(B=\frac{2x_1x_2+3}{x_1^2+x_2^2+2+2x_1x_2}=1\)
\(\Leftrightarrow\frac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=1\)
\(\Leftrightarrow\frac{2m+1}{m^2+2}=1\)
\(\Leftrightarrow m^2-2m+1=0\Rightarrow m=1\)