Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để giá trị phân thức dc xác định thì x2 -1 # 0 <=> x2 # 1 <=> x # 1 và x # -1 ( giải thích: vì muốn phân thức xác định thì mẫu thức phải khác 0)
(mình ko biết ghi dấu "khác" trong toán, nên ghi đỡ dấu thăng nha, sr bạn)
b) Ta có: x2 + 2x +1 / x2 -1
= (x + 1)2 / (x+1).(x-1)
= (x+1).(x+1) / (x+1).(x-1)
= x+1 / x-1
Vậy phân thức rút gọn của phân thức đã cho là x+1/ x-1
de \(\frac{x^2+2x+1}{x^2-1}\)được xác định => x2-1 khác 0 => x khác +-1
\(\frac{x^2+2x+1}{x^2-1}=\frac{\left(x+1\right)^2}{\left(x+1\right).\left(x-1\right)}=\frac{x+1}{x-1}\)

a) ĐK \(\left\{{}\begin{matrix}x-3\ne0\\x+3\ne0\\x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne3\\x\ne-3\\x\ne0\end{matrix}\right.\)
b) \(A=\left(\dfrac{x}{x-3}-\dfrac{x}{x+3}\right).\dfrac{x^2+6x+9}{6x}\)
\(A=\dfrac{x\left(x+3\right)-x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}.\dfrac{\left(x-3\right)^2}{6x}\)
\(A=\dfrac{6x}{\left(x-3\right)\left(x+3\right)}.\dfrac{\left(x-3\right)^2}{6x}=\dfrac{x-3}{x+3}\)
c) \(A=\dfrac{x-3}{x+3}=\dfrac{x+3-6}{x+3}=1-\dfrac{6}{x+3}\)
Để A nguyên khi \(6⋮\left(x+3\right)\Rightarrow\left(x+3\right)\inƯ\left(6\right)=\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
Để A là nguyên dương thì \(\dfrac{6}{x+3}< 1\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=-1\\x+3=-2\\x+3=-3\\x+3=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=-5\\x=-6\\x=-9\end{matrix}\right.\)

Để chứng minh 12n+1/30n+2 là phân số tối giản thì cần chứng tỏ 12n+1 và 30n+2 nguyên tố cùng nhau
Gọi ƯCLN(12n+1,30n+2)=d (d∈N)
=> 12n+1 chia hết cho d => 5(12n+1) chia hết cho d => 60n+5 chia hết cho d
30n+2 chia hết cho d => 2(30n+2) chia hết cho d => 60n+4 chia hết cho d
=> (60n+5)-(60n+4) chia hết cho d
=> 1 chia hết cho d
=> d∈Ư(1)={1}
=> d=1
=> ƯCLN(12n+1,30n+2)=1
Vậy 12n+1/30n+2 là phân số tối giản
k cho mk nha
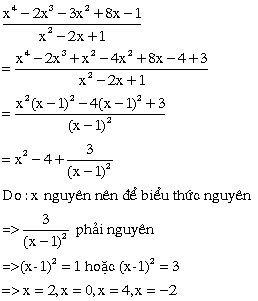
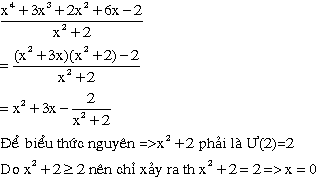 ok bn có thể xem xét mk mk ko chép mạng đâu
ok bn có thể xem xét mk mk ko chép mạng đâu
a) ĐKXĐ: \(n^3+2n^2+2n+1\ne0\)
\(\Rightarrow\left(n+1\right)\left(n^2+n+1\right)\ne0\)
\(\Rightarrow\left\{{}\begin{matrix}n+1\ne0\\n^2+n+1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n\ne-1\\n^2+n+1\ne0\end{matrix}\right.\)
Mà \(n^2+n+1=\left(n^2+n+\frac{1}{4}\right)+\frac{3}{4}=\left(n+\frac{1}{2}\right)^2+\frac{3}{4}>0\)
\(\Rightarrow\) Với mọi giá trị của n thì biểu thức trên lớn hơn 0
\(\Rightarrow n\ne-1\)
b) Ta có: \(n^3+2n^2-1=\left(n+1\right)\left(n^2+n-1\right)\)
Vậy,\(P=\frac{n^3+2n^2+2n+1}{n^3+2n^2-1}=\frac{\left(n+1\right)\left(n^2+n+1\right)}{\left(n+1\right)\left(n^2+n-1\right)}=\frac{n^2+n+1}{n^2+n-1}=1+\frac{2}{n^2-n+1}\)
Để P là phân số tối giản
\(\Leftrightarrow\frac{2}{n^2+n-1}\) là phân số tối giản
\(\Leftrightarrow n^2+n-1⋮̸2\)
Ta có: \(n^2+n=n\left(n+1\right)⋮2\) (vì n và n+1 là 2 số nguyên liên tiếp)
\(\Rightarrow n^2+n-1⋮̸2\)
Như vậy, P là phân số tối giản (điều phải chứng minh).