Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đường thẳng AC qua A ( -2;3 ); C ( 4;1 ) nhận A C → = 6 ; - 2 làm vec tơ chỉ phương nên có phương trình là: x + 2 6 = y - 3 - 2 ⇔ y = - 1 3 x + 7 3
Tọa độ giao điểm của AC và BD là nghiệm của hệ phương trình 3 x - y - 1 = 0 y = - 1 3 x + 7 3 ⇔ x = 1 y = 2
Để ý rằng A C ⊥ B D và I là trung điểm AC.
Khi đó ABCD là hình thoi thì I ( 1;2 ) là trung điểm của BD.
Phương trình hoành độ giao điểm của (C) và d là: 2 x + 1 2 x - m = 3 x - 1 ⇔ 6 x 2 - 3 m + 4 x + m - 1 = 0
Do ∆ = 3 m + 4 2 - 4 . 6 m - 1 = 9 m 2 + 24 > 0 , ∀ m nên d luôn cắt (C) tại hai điểm phân biệt B và D.
Gọi x 1 , x 2 là hai nghiệm của phương trình (*). Theo định lý Viet ta có x 1 + x 2 2 = 3 m + 4 12
Đáp án A
Để I là trung điểm của BD thì 3 m + 4 12 = 1 ⇔ m = 8 3
Đáp án A

Đáp án C
Giả sử ![]()
Hoành độ điểm D là nghiệm phương trình: ![]()
![]()
![]()
![]()
Hoành độ điểm E là nghiệm của phương trình: ![]()
![]()
![]()
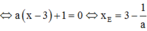
Hoành độ điểm F là nghiệm của phương trình: ![]()
![]()
![]()
![]()
Khi đó 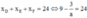
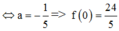

Giả sử z 1 ; z 2 là các nghiệm của phương trình a z 2 + bz + c = 0 với z 1 = 1
Theo định lí Viet ta có:
z 1 z 2 = c a ⇔ z 2 = c a 1 z 1 ⇒ z 2 = c a . 1 z 1 = 1
Bởi vì
z 1 + z 2 = - b a a = b ⇒ z 1 + z 2 2 = 1
Suy ra
z 1 + z 2 z 1 + z 2 1 ⇔ z 1 + z 2 1 z 1 + 1 z 2 = 1 ⇔ z 1 + z 2 2 = z 1 z 2 ⇔ b 2 = a c
Đáp án B



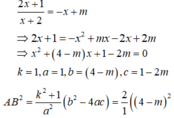
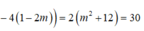


ta có: \(\frac{a}{b}:\frac{c}{d}=\frac{a}{b}.\frac{c}{d}\Leftrightarrow\frac{a}{b}.\frac{d}{c}=\frac{a}{b}.\frac{c}{d}\Leftrightarrow\frac{a.d}{b.c}=\frac{a.c}{bd}\Leftrightarrow\frac{d}{c}=\frac{c}{d}\Leftrightarrow d^2=c^2\)
suy ra d=c hoặc d=-c
suy ra \(\frac{c}{d}=\frac{c}{c}=1\) hoặc \(\frac{c}{d}=\frac{c}{-c}=-1\)