
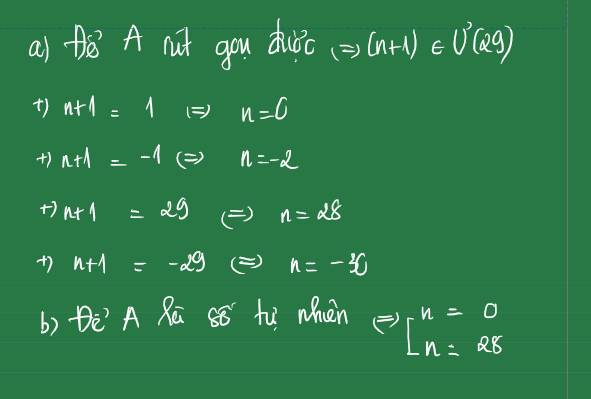
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

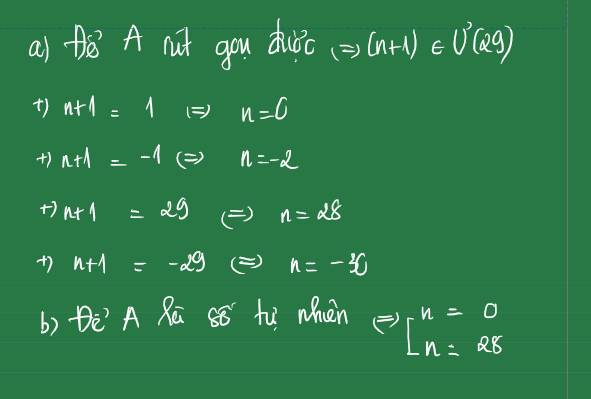

Để \(\frac{63}{3n+1}\) rút gọn được thì 63 và 3n + 1 phải có ước chung
Có \(63=3^2.7\) nên 3n + 1 sẽ có ước là 3 hoặc 7.
Vì 3n+1 không thể chia hết cho 3 với n là số tự nhiên nên 3n+1 sẽ có ước là 7.
Như vậy: \(3n+1=7k\left(k\in Z\right)\)
\(\Leftrightarrow3n=7k-1\)
\(\Leftrightarrow n=\frac{7k-1}{3}\)
\(\Leftrightarrow n=\frac{6k+k-1}{3}\)
\(\Leftrightarrow n=2k+\frac{k-1}{3}\)
Vậy để n là số tự nhiên thì \(\frac{k-1}{3}\in N\) hay k = 3a+1. Thay vào biểu thức n ta có:
\(n=\frac{7k-1}{3}=\frac{7\left(3a+1\right)-1}{3}=7a+2\)
Vậy n = 7a+2 thì thỏa mãn đề bài.
P/s: không biết đúng hay không thôi nhé

a. Ta có \(63=3^2.7\) có 2 ước nguyên tố là 3 và 7
Do \(3n+1\) ko chia hết cho 3 với mọi n tự nhiên
\(\Rightarrow\) Phân số đã cho rút gọn được khi \(3n+1\) và 63 có ước chung là 7
\(\Rightarrow3n+1⋮7\)
Mà 3n+1 và 7 đều chia 3 dư 1 \(\Rightarrow3n+1=7\left(3k+1\right)\Rightarrow n=7k+2\) với k là số tự nhiên
Vậy \(n=7k+2\) với k là số tự nhiên thì phân số đã cho rút gọn được
b.
A là số tự nhiên khi \(63⋮3n+1\Rightarrow3n+1=Ư\left(63\right)\)
Mà \(3n+1⋮̸3\Rightarrow\left[{}\begin{matrix}3n+1=7\\3n+1=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}n=2\\n=0\end{matrix}\right.\)

A)Để A được rút gọn thì 3n+1 là ước của 63
=>3n + 1 thuộc {63;-1;1;-63}
=>n thuộc ...
b|) Tương tự

Để \(\frac{63}{3n+1}\) rút gọn được thì 63 và 3n + 1 phải có ước chung.
Có \(63=3^2.7\)nên 3n + 1 sẽ có ước là 3 hoặc 7.
Bởi vì 3n + 1 không thể chia hết cho 3 với n là số tự nhiên nên 3n + 1 sẽ có ước là 7.
Như vậy : \(3n+1=7k\left(k\in Z\right)\)
\(\Leftrightarrow3n=7k-1\)
\(\Leftrightarrow n=\frac{7k-1}{3}\)
\(\Leftrightarrow n=\frac{6k+k-1}{3}\)
\(\Leftrightarrow n=2k+\frac{k-1}{3}\)
Vậy để n là số tự nhiên thì \(\frac{k-1}{3}\in N\) hay \(k=3a+1\). Thay vào biểu thức n ta có:
\(n=\frac{7k-1}{3}=\frac{7\left(3a+1\right)-1}{3}=7a+2.\)
Vậy n = 7a + 2 thì thỏa mãn đề bài.