Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

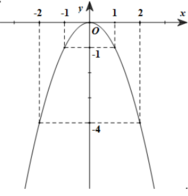
a, Bảng giá trị
x |
-2 |
-1 |
0 |
1 |
2 |
y = –x2 |
-4 |
-1 |
0 |
-1 |
-4 |
Đồ thị:
b) Xét phương trình hoành độ giao điểm của (d) và (P): –x2 = 4x – m ⇔ x2 + 4x – m = 0 (1)
(d) và (P) có đúng 1 điểm chung ⇔ phương trình (1) có nghiệm kép ⇔ ∆’ = 22 – (–m) = 0
ó 4 + m = 0 ⇔ m = –4
Vậy m = –4

phương trình hoành độ giao điểm : x2 = 2x + a \(\Leftrightarrow x^2-2x-a=0\) (1)
vì d và (p) không có điểm chung nên phương trình (1) vô nghiệm
\(\Leftrightarrow\Delta^'^{ }<0\Leftrightarrow1+a<0\Leftrightarrow a<-1\)
vậy với a<-1 thì d và (p) không có điểm chung

Phương trình hoành độ giao điểm của (P) với (d):
\(\frac{-1}{4}x^2=\left(m+1\right)x+m^2+3\)
\(\Leftrightarrow x^2+4\left(m+1\right)x+4m^2+12=0\)
\(\Delta'=2^2\left(m+1\right)^2-4m^2-12\)
\(=4m^2+8m+4-4m^2-12\)
\(=8m-8\)
(P) và (d) không có điểm chung khi pt hoành độ giao điểm vô nghiệm.
\(\Leftrightarrow\Delta'< 0\Leftrightarrow8m-8< 0\)
\(\Leftrightarrow m< 1\)
Phương trình hoành độ giao điểm của (p) và (d) là
\(-\frac{1}{4}x^2=\left(m+1\right)x+m^2+3\)<=> \(\frac{1}{4}x^2+\left(m+1\right)x+m^2+3=0\)
\(\left(a=\frac{1}{4},b=m+1,c=m^2+3\right)\)
\(\Delta=b^2-4ac=\left(m+1\right)^2-4\cdot\frac{1}{4}\left(m^2+3\right)\)
\(=m^2+2m+1-m^2-3=2m-2\)
(p) và (d) không có điểm chung <=> \(\Delta< 0\)
<=> \(2m-2< 0\)<=> \(2m< 2\)<=> \(m< 1\)
Vậy với \(m< 1\)thì (p) và (d) không có điểm chung

a: PTHĐGĐ là:
x^2+mx-m-2=0(1)
Khi m=2 thì (1) sẽ là
x^2+2x-2-2=0
=>x^2+2x-4=0
=>\(\left[{}\begin{matrix}x=-1+\sqrt{5}\\x=-1-\sqrt{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=6-2\sqrt{5}\\y=6+2\sqrt{5}\end{matrix}\right.\)
b: Δ=m^2-4(-m-2)
=m^2+4m+8
=(m+2)^2+4>0 với mọi x
=>(d) luôn cắt (P) tại hai điểm phân biệtx
x1^2+x2^2=7
=>(x1+x2)^2-2x1x2=7
=>(-m)^2-2(-m-2)=7
=>m^2+2m+4-7=0
=>m^2+2m-3=0
=>m=-3 hoặc m=1

Thay x=-1 vào (P), ta được:
y=-2*(-1)^2=-2
Thay x=-1và y=-2 vào (d), ta được:
-(m+1)-m-3=-2
=>-m-1-m-3=-2
=>-2m-4=-2
=>2m+4=2
=>m=-1

Xét phương trình hoành độ giao điểm có :
\(-x^2=4x-m\Leftrightarrow x^2-4x-m=0\)
để hai đồ thị cắt tại đúng một điểm thì phương trình hoành đọ giao điểm có nghiệm kép hay
\(\Delta^'=2^2+m=0\Leftrightarrow m=-4\)

a: PTHĐGĐ là;
x^2-(2m-3)x+m^2-3m=0
Δ=4m^2-12m+9-4m^2+12m=9>0
=>(P) luôn cắt (d) tại hai điểm pb
b: |x1|+|x2|=3
=>x1^2+x2^2+2|x1x2|=9
=>(2m-3)^2-2(m^2-3m)+2|m^2-3m|=9
TH1: m>=3 hoặc m<=0
=>(2m-3)^2=9
=>m=3(nhận) hoặc m=0(nhận)
Th2: 0<m<3
=>4m^2-12m+9-4(m^2-3m)=9
=>4m^2-12m-4m^2+12m=0
=>0m=0(luôn đúng)

Phương trình hoành độ giao điểm d và (P):
\(-2x^2=x-m\Leftrightarrow2x^2+x-m=0\) (1)
(d) cắt (P) tại 2 điểm pb khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=1+8m>0\Leftrightarrow m< -\dfrac{1}{8}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{1}{2}\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Leftrightarrow-\dfrac{1}{2}=-\dfrac{m}{2}\Leftrightarrow m=1\)
Phương trình hoành độ giao điểm:
\(x^2=2x+a\Leftrightarrow x^2-2x-a=0\) (1)
d và (P) không có điểm chung khi và chỉ khi (1) vô nghiệm
\(\Leftrightarrow\Delta'=1+a< 0\Rightarrow a< -1\)
Phương trình hoành độ giao điểm là:
\(x^2=2x+a\)
\(\Leftrightarrow x^2-2x-a=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot\left(-a\right)=4a+4\)
Để phương trình vô nghiệm thì 4a+4<0
hay a<-1