Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(MF = \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} ,d\left( {M,\Delta } \right) = \left| {y + 1} \right|\).
Xét \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = \left| {y + 1} \right| \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {y + 1} \right)^2} \Leftrightarrow {x^2} = 4y \Leftrightarrow y = \frac{1}{4}{x^2}\).
Vậy tập hợp điểm M để \(MF{\rm{ }} = \;d\left( {M,\Delta } \right)\) là parabol \(y = \frac{1}{4}{x^2}\)

Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.

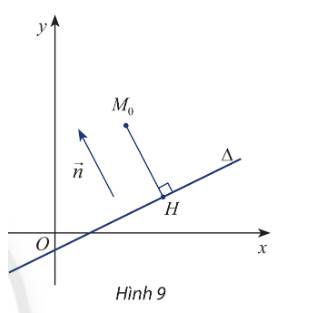
a) Ta có: \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Mà H là hình chiếu vuông góc của \({M_0}\) trên \(\Delta \) nên \(H{M_0} \bot \Delta \)
Mặt khác vectơ pháp tuyến \(\overrightarrow n \) cùng vuông góc với \(\Delta \)
Suy ra \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \)cùng phương (đpcm)
b) Ta có: \(\overrightarrow n = (a;b)\) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Suy ra \(p = \overrightarrow n .\overrightarrow {H{M_0}} = a\left( {{x_0} - {x_H}} \right) + b\left( {{y_0} - {y_H}} \right) = a{x_0} + b{y_0} - \left( {a{x_H} + b{y_H}} \right)\) (1)
Mà H thuộc đường thẳng \(\Delta \) nên tọa độ điểm H thỏa mãn phương trình đường thẳng \(\Delta \)
Thay tọa độ điểm H vào phương trình \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) ta có:
\(a{x_H} + b{y_H} + c = 0 \Leftrightarrow c = - \left( {a{x_H} + b{y_H}} \right)\)
Thay \(c = - \left( {a{x_H} + b{y_H}} \right)\) vào (1) ta có
\(p = a{x_0} + b{y_0} + c\) (đpcm)
c) Ta có: \(p = \overrightarrow n .\overrightarrow {H{M_0}} \Leftrightarrow \overrightarrow {H{M_0}} = \frac{p}{{\overrightarrow n }} \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \left| {\frac{p}{{\overrightarrow n }}} \right| \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\)

Tọa độ điểm A, B là nghiệm của hệ phương trình :
\(\begin{cases}\left(x+1\right)^2+\left(y-2\right)^2=13\\x-5y-2=0\end{cases}\) \(\Leftrightarrow\begin{cases}26y^2+26y=0\\x=5y+2\end{cases}\)
\(\Leftrightarrow\begin{cases}\begin{cases}x=2\\y=0\end{cases}\\\begin{cases}x=-3\\y=-1\end{cases}\end{cases}\)
\(\Rightarrow A\left(2;0\right);B\left(-3;-1\right)\) hoặc \(A\left(-3;-1\right);B\left(2;0\right)\)
Vì tam giác ABC vuông tại B và nội tiếp đường tròn (C) nên AC là đường kính của đường tròn (C). Hay tâm \(I\left(-1;2\right)\) là trung điểm của AC
Khi đó : \(A\left(2;0\right);B\left(-3;-1\right)\Rightarrow C\left(-4;4\right)\)
\(A\left(-3;-1\right);B\left(2;0\right)\Rightarrow C\left(1;5\right)\)
Vậy \(C\left(-4;4\right)\) hoặc \(C\left(1;5\right)\)

a) Ta có: \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1 \Leftrightarrow x - 2y + 4 = 0\)
Vậy khoảng cách từ O đến \(\Delta \) là: \(d\left( {O;\Delta } \right) = \frac{{\left| {1.0 - 2.0 + 4} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \frac{{4\sqrt 5 }}{5}\)
b) Lấy \(M\left( {0;1} \right) \in {\Delta _1}\)
Suy ra: \(d\left( {{\Delta _1},{\Delta _2}} \right) = d\left( {M,{\Delta _2}} \right) = \frac{{\left| {0 - 1 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 \)

\(F\left(x\right)=sin\left(2\pi-\frac{\pi}{2}+x\right)+cos\left(14\pi-\frac{\pi}{2}-x\right)+sin\left(2x+\pi+x\right)-cos\left(6\pi+\pi-x\right)\)
\(=-sin\left(\frac{\pi}{2}-x\right)+cos\left(\frac{\pi}{2}+x\right)+sin\left(\pi+x\right)-cos\left(\pi-x\right)\)
\(=-cosx-sinx-sinx+cosx=-2sinx\)
b/ \(F\left(x\right)=-1\Leftrightarrow-2sinx=-1\)
\(\Rightarrow sinx=\frac{1}{2}\Rightarrow x=30^0\)
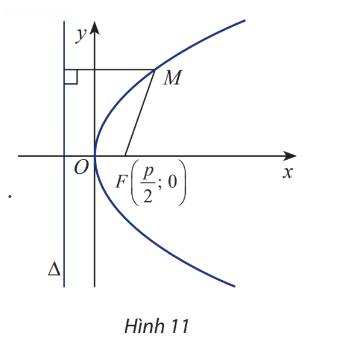

a) Ta có: \(\overrightarrow {FM} = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} \)
\(d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|\)
b) M thuộc parabol (P) nên M cách đều F và \(\Delta \)
Suy ra \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x - \frac{p}{2}} \right|\)