Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Sửa đề: \(EM\cdot AM=MF\cdot OA\)
\(\widehat{EMO}=\widehat{EMF}+\widehat{OMF}\)
=>\(\widehat{EMF}+\widehat{OMF}=90^0\)(1)
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMO}+\widehat{FMO}=\widehat{AMF}=90^0\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{EMF}=\widehat{AMO}\)
=>\(\widehat{EMF}=\widehat{OAM}\)
ΔMEO vuông tại M
=>\(\widehat{MEO}+\widehat{MOE}=90^0\)
=>\(\widehat{MEF}+\widehat{MOE}=90^0\)(3)
Ta có: OM nằm giữa OA và OE
=>\(\widehat{AOM}+\widehat{MOE}=90^0\)(4)
từ (3) và (4) suy ra \(\widehat{MEF}=\widehat{AOM}\)
Xét ΔMEF và ΔAOM có
\(\widehat{MEF}=\widehat{AOM}\)
\(\widehat{EMF}=\widehat{OAM}\)
Do đó: ΔMEF đồng dạng với ΔAOM
=>ME/AO=MF/AM
=>\(ME\cdot AM=AO\cdot MF\)
b: Xét (O) có
ΔAIB nội tiếp
AB là đường kính
Do đó: ΔAIB vuông tại I
=>AI\(\perp\)SB
Xét ΔSAB có
BM,SO là đường cao
BM cắt SO tại F
Do đó; F là trực tâm
=>AF\(\perp\)SB
mà AI\(\perp\)SB(cmt)
và AF,AI có điểm chung là A
nên A,I,F thẳng hàng

#)Giải :
Có \(\widehat{AMB}=90^o\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{OMA}+\widehat{OMT}=\widehat{AMB}=90^o\)
MF là tiếp tuyến của (O) \(\Rightarrow\widehat{OMF}=90^o\Rightarrow\widehat{OMT}+\widehat{TMF}=\widehat{OMF}=90^o\)
\(\Rightarrow\widehat{OMA}=\widehat{TMF}\left(1\right)\)
Dễ c/m \(\Delta BAM~\Delta BOT\Rightarrow\left(g.g\right)\widehat{OAM}=\widehat{OTB}\)
Mà \(\widehat{OCB}=\widehat{MTF}\left(đđ\right)\Rightarrow\widehat{OAM}=\widehat{MTF}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\Delta OMA~\Delta FMT\left(g.g\right)\Rightarrow\frac{MA}{MT}=\frac{OA}{OF}\Rightarrow MA.FT=OA.MT\)
b) Có \(\Delta OMA~\Delta FMT\left(cmt\right)\)
Mà \(\Delta OMA\) cân tại O
\(\Rightarrow\Delta FMT\) cân tại F
\(\Rightarrow FM=FT\) (cặp cạnh t/ứng = nhau)
Lại có \(\Delta TME\) vuông tại M \(\Rightarrow FM=FE\)
c) Dễ c/m được TA = TB
Mà \(\Delta MTE~\Delta OTB\left(g.g\right)\Rightarrow\frac{ME}{OB}=\frac{TE}{TB}\Rightarrow ME.TB=OB.TE\Rightarrow ME.TA=2R^2\left(TE=2MF=2R\right)\)

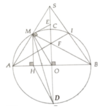
a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC

@Nguyễn Việt Lâm@Khôi Bùi@Truong Viet Truong@Akai Haruma@Phùng Tuệ Minh@DƯƠNG PHAN KHÁNH DƯƠNG@saint suppapong udomkaewkanjana
A B C T D O E M F
lời giải vắn tắt:
a) \(\widehat{AMB}\)là góc nội tiếp chắn nửa đường tròn => \(\widehat{AMB}=90^o\)
=>\(\widehat{OMA}+\widehat{OMT}=\widehat{AMB}=90^o\)
MF là tiếp tuyến của (O)=> \(\widehat{OMF}=90^o\rightarrow\widehat{OMT}+\widehat{TMF}=\widehat{OMF}=90^o\)
=> \(\widehat{OMA}=\widehat{TMF}\)(1)
\(\Delta MAB\)~\(\Delta OTB\)(g.g)(tự cm)=>\(\widehat{OAM}=\widehat{OTB}\)
mà \(\widehat{OCB}=\widehat{MTF}\)(đối đỉnh) =>\(\widehat{OAM}=\widehat{MTF}\)(2)
từ (1) và (2)=> \(\Delta OMA\)~\(\Delta FMT\)(g.g)\(\rightarrow\frac{MA}{MT}=\frac{OA}{FT}\rightarrow MA.FT=OA.MT\)
b)\(\Delta OMA\)~\(\Delta FMT\)(cmt ) mà \(\Delta OMA\)cân ở O=> \(\Delta FMT\)cân ở F
=> FM=FT
mà \(\Delta TME\) vuông ở M => ..... FM=FE
c) ta cm được TA=TB
lại có:\(\Delta MTE\)~\(\Delta OTB\)(g.g) \(\rightarrow\frac{ME}{OB}=\frac{TE}{TB}\)\(\rightarrow ME.TB=OB.TE\)
\(\rightarrow ME.TA=R.2R=2R^2\)(TE=2FM=2R)
Thanks nha