Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

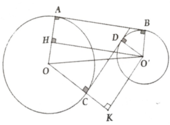
Kẻ O’H ⊥ OA; O’K ⊥ OC
OH = 4; OK = 8
Đặt CD = x => AB = 2x
O O ' 2 = 64 + x 2
và O O ' 2 = 16 + 4 x 2
=> x = 4 => OO' = 80 cm

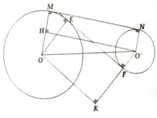
a, Kẻ O'H ⊥ OM; OK ⊥ O'F
có OH = R – r; O’K = R + r
Mà O H 2 = O O ' 2 - M N 2 = 36
O ' K 2 = O O ' 2 - E F 2 = 64
=> OH = 6 và O'K = 8
=> R = 7cm và r = 1cm
b, R = 17 2 cm và r = 7 2 cm

a, 700 góc nào bạn ?
b, Vì AB là tiếp tuyến (O) => ^ABO = 900
AO giao BC = K
AB = AC ; OB = OC = R
Vậy OA là đường trung trực đoạn BC
Xét tam giác ABO vuông tại B, đường cao BK
Áp dụng định lí Pytago tam giác ABO vuông tại B
\(AB=\sqrt{AO^2-BO^2}=\sqrt{16-4}=2\sqrt{3}\)cm
Áp dụng hệ thức : \(BK.AO=BO.AB\Rightarrow BK=\frac{BO.AB}{AO}=\frac{4\sqrt{3}}{4}=\sqrt{3}\)cm
Vì AO là đường trung trực => \(BC=2KB=2\sqrt{3}\)cm
Chu vi tam giác ABC là :
\(P_{ABC}=AB+AC+BC=2AB+BC=4\sqrt{3}+2\sqrt{3}=6\sqrt{3}\)cm

Câu a, ta có Id=Ie là tiếp tuyến cắt nhau tại I.
-> ID=IA (1)
Cmtt -> IE=IA(2)
TỪ (1)-(2) ta có id=ie=ia
Trung tuyến ia=1/2 de
-> dea vuông tại a
-> dea = 90*