Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$(O), (O')$ tiếp xúc ngoài tại $A$ thì $O,A,O'$ thẳng hàng.
$OM\perp MN, O'N\perp MN$ (do $MN$ là ttc)
$\Rightarrow MNO'O$ là hình thang
$\Rightarrow \widehat{NO'A}+\widehat{MOA}=180^0$ (2 góc trong cùng phía).
Lại có:
Theo tính chất tiếp tuyến, góc thì:
$\widehat{AMN}= \frac{1}{2}\widehat{MOA}$
$\widehat{ANM}=\frac{1}{2}\widehat{NO'A}$
$\Rightarrow \widehat{AMN}+\widehat{ANM}=\frac{1}{2}(\widehat{MOA}+\widehat{NO'A})$
$=\frac{1}{2}.180^0=90^0$
$\Rightarrow \widehat{MAN}=90^0$
b. Từ $A$ kẻ tiếp tuyến $AT$ chung của $(O), (O')$
Theo tính chất 2 tt cắt nhau thì:
$AT=MT=TN$
$\Rightarrow MN=MT+TN= 2AT$
Cũng theo tính chất 2 tiếp tuyến cắt nhau thì $TO, TO'$ lần lượt là phân giác $\widehat{MTA}, \widehat{NTA}$
Mà $\widehat{MTA}+\widehat{NTA}=180^0$ nên $TO\perp TO'$
Tam giác $TOO'$ vuông có đường cao $TA$, áp dụng HTL:
$TA^2=OA.O'A=9.4=36$
$\Rightarrow TA=6$
$MN=2TA=2.6=12$ (cm)

1 2 1 2 3 4 B I C O A O'
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC .
Tam giác ABC có đường trung tuyến \(AI=\frac{1}{2}BC\)nên là tam giác vuông
Vậy \(\widehat{BAC}=90^o\left(đpcm\right)\)
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên :
\(\widehat{OIO'}=\widehat{OIA}+\widehat{O'IA}=\frac{1}{2}\widehat{AIB}+\frac{1}{2}\widehat{AIC}=\frac{1}{2}\left(\widehat{AIB}+\widehat{AIC}\right)\)
Vậy : \(\widehat{OIO'}=90^o\)
c) \(\Delta OIO'\) vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9 . 4 = 36
=> IA = 6 ( cm )
Vậy BC = 2 . IA = 2 . 6 = 12 (cm)

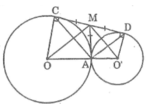
Ta có :
MO là tia phân giác của góc (CMA) (tính chất hai tiếp tuyến cắt nhau)
MO’ là tia phân giác của góc (DMA) (tính chất hai tiếp tuyến cắt nhau)
Suy ra : MO ⊥ MO’ (tính chất hai góc kề bù)
Tam giác MOO’ vuông tại M có MA ⊥ OO’ (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có :
M A 2 = OA.O’A = 4,5.2 = 9 ⇒ MA = 3 (cm)
Mà MA = 12 CD ⇒ CD = 2.MA = 2.3 = 6 (cm)
a: Gọi AH là tiếp tuyến chung của hai đường tròn (O) và (O'), H∈MN
Xét (O) có
HM,HA là các tiếp tuyến
Do đó: HM=HA và HO là phân giác của góc MHA
Xét (O') có
HA,HN là các tiếp tuyến
Do đó: HA=HN và HO' là phân giác của góc AHN
Ta có: HM=HA
HN=HA
Do đó: HM=HN
=>H là trung điểm của MN
Xét ΔAMN có
AH là đường trung tuyến
\(AH=\dfrac{MN}{2}\)
Do đó: ΔAMN vuông tại A
=>\(\widehat{MAN}=90^0\)
b: HO là phân giác của góc MHA
=>\(\widehat{MHA}=2\cdot\widehat{OHA}\)
HO' là phân giác của góc AHN
=>\(\widehat{AHN}=2\cdot\widehat{AHO'}\)
Ta có: \(\widehat{MHA}+\widehat{NHA}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{OHA}+\widehat{O'AH}\right)=180^0\)
=>\(2\cdot\widehat{OHO'}=180^0\)
=>\(\widehat{OHO'}=90^0\)
Xét ΔHO'O vuông tại H có HA là đường cao
nên \(HA^2=OA\cdot O'A\)
=>\(HA^2=9\cdot4=36\)
=>\(HA=\sqrt{36}=6\left(cm\right)\)
MN=2*HA
=>MN=2*6=12(cm)