Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét (O) có
ΔBAC nội tiếp đường tròn
AB là đường kính
Do đó: ΔBAC vuông tại C
Xét (O) có
OE là một phần đường kính
BC là dây
E là trung điểm của BC
Do đó: OE\(\perp\)BC tại E
c: Xét ΔDEC vuông tại E và ΔDEB vuông tại E có
DE chung
CE=BE
Do đó: ΔDEC=ΔDEB
Suy ra: DC=DB
Xét ΔOCD và ΔOBD có
OC=OB
DC=DB
OD chung
Do đó: ΔOCD=ΔOBD
Suy ra: \(\widehat{OCD}=\widehat{OBD}\)
\(\Leftrightarrow\widehat{OCD}=90^0\)
hay DB là tiếp tuyến của (O)

b: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔABC vuông tại C
Xét ΔABC có
O là trung điểm của AB
E là trung điểm của BC
Do đó: OE là đường trung bình của ΔBAC
Suy ra: OE\(\perp\)CB
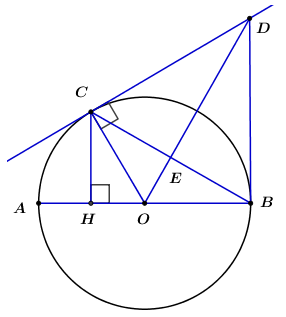
a) Xét đường tròn (O) có AB là đường kính và △ ABC nội tiếp đường tròn (O)
⇒ \(\widehat{ACB}=90^0\) hay △ ABC vuông tại C.
Có: OC = OB (do cùng bằng bán kính), suy ra O cách đều hai điểm C và B,
⇒ O nằm trên trung trực của BC.
Có EC = EB (do E là trung điểm của BC), suy ra E cách đều hai điểm B và C
⇒ E nằm trên trung trực của BC.
Ta có E và O đều nằm trên đường trung trực của đoạn BC
⇒ OE là trung trực của đoạn BC.
⇒ OE ⊥ BC (đpcm)
b) Vì tiếp tuyến tại C của (O) cắt OE ở D nên ta có D nằm trên EO, suy ra D nằm trên đường trung trực của BC ⇒ DB = DC (tính chất đường trung trực)
Xét ΔCOD và ΔBOD có:
OC = OB (do cùng là bán kính của đường tròn)
OD chung
DB = DC (cmt)
⇒ ΔCOD = ΔBOD ( c − c − c )
⇒ \(\widehat{OCD}=\widehat{OBD}=90^0\)
⇒ BD ⊥ OB
Suy ra DB là tiếp tuyến của (O) (đpcm).
c)Vì DB là tiếp tuyến của (O) (cmt)
⇒ \(\widehat{OBD}=90^0\) ⇒ \(\widehat{CBO}+\widehat{CBD}=90^0\) \(\left(1\right)\)
Vì OD là trung trực của BC (cmt)
⇒ OD ⊥ BC ⇒ \(\widehat{DEB}=90^0\)⇒ \(\widehat{ODB}+\widehat{CBD}=90^0\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ⇒ \(\widehat{CBO}=\widehat{ODB}\) ( cùng phụ với \(\widehat{DBC}\) )
Xét △ ODB và △ CBH có:
\(\widehat{CHB}=\widehat{OBD}=90^0\)
\(\widehat{CBO}=\widehat{ODB}\) ( cmt )
⇒ △ ODB \(\approx\) △ CBH ( g − g )
⇒ \(\dfrac{OB}{CH}=\dfrac{OD}{BC}\)
⇒ OB . BC = OD . CH
⇒ △ ODB ∼ △ CBH ( g − g )
Mà có OB = OC (do cùng là bán kính của đường tròn)
Suy ra: CB.OC=OD.HC (đpcm)

b: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔABC vuông tại C
Xét (O) có
OE là một phần đường kính
CB là dây
E là trung điểm của CB
Do đó: OE\(\perp\)BC
c: Xét ΔDEC vuông tại E và ΔDEB vuông tại E có
DE chung
EC=EB
Do đó: ΔDEC=ΔDEB
Suy ra: DC=DB
Xét ΔOCD và ΔOBD có
OC=OB
OD chung
CD=BD
Do đó: ΔOCD=ΔOBD
Suy ra: \(\widehat{OCD}=\widehat{OBD}\)
mà \(\widehat{OCD}=90^0\)
nên \(\widehat{OBD}=90^0\)
hay DB\(\perp\)OB tại B
hay DB là tiếp tuyến của (O)

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
ΔOBC cân tại O
mà OE là trung tuyến
nên OE vuông góc với BC và OE là phân giác của góc BOC
b: Xét ΔOBD và ΔOCD có
OB=OC
góc BOD=góc COD
OD chung
Do đó: ΔOBD=ΔOCD
=>góc OBD=90 độ
=>DB là tiếp tuyên của (O)

E C M K I H A B O
a . Ta có : \(C\in\left(O\right),AB=2R\Rightarrow\widehat{ACB}=90^0\Rightarrow\Delta ABC\) vuông tại C
c . Vì \(OK\perp BC\Rightarrow B,C\) đối xứng qua OK
\(\Rightarrow\widehat{DCO}=\widehat{DBO}=90^0\Rightarrow DC\) là tiếp tuyến của (O)
d . Ta có \(AC=R\Rightarrow\Delta AOC\) đều
\(\Rightarrow\widehat{COM}=\widehat{MOB}=60^0\Rightarrow\Delta OCM,OMB\) đều
\(\Rightarrow OC=OM=OB=MB=MC\)=> ◊OBMC là hình thoi
e . Ta có :
\(\Delta ACO\) đều
\(\Rightarrow CH==\frac{R\sqrt{3}}{2}\Rightarrow CI=IH=\frac{R\sqrt{3}}{4}\)
\(\Rightarrow\frac{CI}{DB}=\frac{CI}{BC}=\frac{\frac{R\sqrt{3}}{4}}{R\sqrt{3}}=\frac{1}{4}=\frac{AH}{AB}=\frac{EI}{EB}\)
\(\Rightarrow\Delta ECI~\Delta EDB\left(c.g.c\right)\Rightarrow\widehat{CEI}=\widehat{DEB}\Rightarrow E,C,D\) thẳng hàng

A B O C k D H E I M
a) xét tam giác ABC nội tiếp đường tròn (O) có cạnh AB là đường kính =>tam giác ABC vuông tại C
b) có tam giác ABC vuông tại C từ pitago ta có
AB\(^2\)=AC\(^2\)+BC\(^2\)=>BC=\(\sqrt{AB^2-AC^2}=\sqrt{4R^2-R^2}=R\sqrt{3}\)
tam giác AOC có AC=AO=CO=R => tam giác AOC đều =>
\(\widehat{CAO}=60\)độ =>góc CBA = 30 độ (tam giác ABC vuông tại C)
c)xét tam giác COB có OC=OB=R=>tam giác COB cân tại O có OK vừa là trung tuyến (k là trung điểm CB) vừa là phân giác
=>góc COK=góc BOK hay góc COD=góc BOD
xét 2 tam giác COD và BOD có OC=OB, góc COD=góc BOD,OD là cạnh chung
tam giác COD = tam giác BOD(c-g-c) =>góc DCO=góc DBO=90 độ
mà OC = R =>CD là tiếp tuyến of (O)
d) Vì OC=OB,DC=DB=> OD là đường trung trực of BC mà M thuộc OD =>MC=MB (1)OD vuông góc CB => góc CKM = 90 độ
Tam giác CKO vuông tại K từ pitago có OK = \(\sqrt{CO^2-CK^2}=\sqrt{CO^2-\frac{BC^2}{4}}=\sqrt{R^2-\frac{3R^2}{4}}=\frac{R}{2}\)
=> KM = OM - OK = R - \(\frac{R}{2}=\frac{R}{2}\)=OK
tương tự xét tam giác CMK vuông tại K có CM =R (2)
có OC=OB (3)
Từ ( 1 ) ; (2);(3) => OC = CM =MB = OB =R =>Tứ giác OCMB là hình thoi
e) Tương tự câu b ta có tam giác EAO = ECO ( c-g-c)
=> Góc ECO = Góc EAO = 90 độ .
Ta có : Góc ECD = Góc ECO + Góc OCD = 90 độ + 90 độ = 180 độ
=> E ; C ; D thẳng hàng
Bạn OOOĐỒ DỐI TRÁ OOO ơi , cho mình hỏi là phần d í , tại sao OK = Căn của R^2 - BC^2 / 4 nnhir ? Mình không hiểu đoạn BC^2 / 4
b: Xét (O) có
ΔBAC nội tiếp đường tròn
AB là đường kính
Do đó: ΔBAC vuông tại C
Xét (O) có
OE là một phần đường kính
BC là dây
E là trung điểm của BC
Do đó: OE\(\perp\)BC
c: Xét ΔDEC vuông tại E và ΔDEB vuông tại E có
DE chung
CE=BE
Do đó: ΔDEC=ΔDEB
Suy ra: DC=DB
Xét ΔOBD và ΔOCD có
OB=OC
OD chung
DB=DC
Do đó: ΔOBD=ΔOCD
Suy ra: \(\widehat{OBD}=\widehat{OCD}\)
\(\Leftrightarrow\widehat{OBD}=90^0\)
hay DB là tiếp tuyến có B là tiếp điểm của (O)