Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

viết đề sai rùi bạn
b) chứng minh tứ giác POMQ LÀ hình chữ nhật chứ ko phải chứng minh AQMO LÀ HÌNH CHỮ NHẬT OK

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC

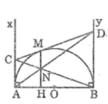
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: ND/NA = BD/AC (hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: ND/NA = MD/MC
Trong tam giác ACD, ta có: ND/NA = MD/MC
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: AC ⊥ AB (vì Ax ⊥ AB)
Suy ra: MN ⊥ AB

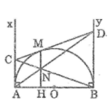
Trong tam giác ACD, ta có: MN // AC
Suy ra: MN/AC = DN/DA (hệ quả định lí Ta-lét) (3)
Trong tam giác ABC, ta có: MH // AC (vì M, N, H thẳng hàng)
Suy ra: HN/AC = BN/BC (hệ quả định lí Ta-lét) (4)
Trong tam giác BDN, ta có: AC // BD
Suy ra: ND/NA = BN/NC (hệ quả định lí Ta-lét)
⇒ ND/(DN + NA) = BN/(BN + NC) ⇔ ND/DA = BN/BC (5)
Từ (3), (4) và (5) suy ra: MN/AC = HN/AC ⇒ MN = HN

a, Vì CA = CM ( tc tiếp tuyến cắt nhau )
OA = OM = R
=> OC là đường trung trực đoạn AM
=> OC vuông AM
^AMB = 900 ( góc nội tiếp chắn nửa đường tròn )
=> AM vuông MB (1)
Ta có : DM = DB ( tc tiếp tuyến cắt nhau )
OM = OB = R
=> OD là đường trung trực đoạn MB
=> OD vuông MB (2)
Từ (1) ; (2) => OD // AM
b, OD giao MB = {T}
OC giao AM = {U}
Xét tứ giác OUMT có ^OUM = ^UMT = ^MTO = 900
=> tứ giác OUMT là hcn => ^UOT = 900
Vì CD là tiếp tuyến (O) với M là tiếp điểm => ^OMD = 900
Mặt khác : BD = DM ( tc tiếp tuyến cắt nhau )
CM = AC ( tc tiếp tuyến cắt nhau )
Xét tam giác COD vuông tại O, đường cao OM
Ta có : \(OM^2=CM.MD\)hay \(OM^2=AC.BD\)=> R^2 = AC.BD
c, Gọi I là trung điểm CD
O là trung điểm AB
khi đó OI là đường trung bình hình thang BDAC
=> OI // AC mà AC vuông AB ( tc tiếp tuyến ) => OI vuông AB
Xét tam giác COD vuông tại O, I là trung điểm => OI = IC = ID = R
Vậy AB là tiếp tuyến đường tròn (I;CD/2)

