Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
MA.MC là tiếp tuyến
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại E
góc ADB=1/2*180=90 độ
=>góc ADM=90 độ=góc AEM
=>AMDE nội tiếp
b: AMDE nội tiếp
=>góc ADE=góc AMO=góc ACO

a: góc MAO+góc MCO=180 độ
=>MAOC nội tiếp
góc ADB=1/2*sđ cung AB=90 độ
=>AD vuông góc MB
Xét (O) có
MA,MC là tiếp tuyến
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại E
góc ADM=góc AEM=90 độ
=>AEDM là tứ giác nội tiếp

O A B x C E D M
a, xét tg AEO và CEO có : EO chung
^AEO = ^CEO = 90
OA = OC = r
=> Tg AEO = tg CEO (ch-cgv)
=> ^AOE = ^COE
xét tg MAO và tg MCO có : Mo chung
OA = OC = r
=> tg MAO = tg MCO (cg-c)
=> ^MAO = ^MCO
mà ^MAO = 90
=> ^MCO = 90 => OC _|_ MC
có C thuộc 1/2(o)
=> MC là tt của 1/2(o)
b, xét tứ giác MCOA có : ^MCO = ^MAO = 90
=> ^MCO + ^MAO = 180
=>MCOA nội tiếp
+ có D thuộc 1/(o) dk AB (gt) => ^ADB = 90 = ADM
có MEA = 90 do AC _|_ MO (Gt)
=> ^ADM = ^MEA = 90
=> MDEA nt
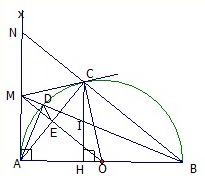


a: góc MAO+góc MCO=90+90=180 độ
=>MAOC nội tiếp
b: Xét (O) có
MA,MC là tiếp tuyến
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC