Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Ta có: CM+MD=CD
nên CD=AC+BD
2: Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
3: Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
hay \(AC\cdot BD=\left(\dfrac{AB}{2}\right)^2=\dfrac{AB^2}{4}\)
4: Ta có: CM=CA
nên C nằm trên đường trung trực của MA(3)
Ta có: OM=OA
nên O nằm trên đường trung trực của MA(4)
Từ (3) và (4) suy ra OC\(\perp\)MA(5)
Xét (O) có
ΔMAB nội tiếp
AB là đường kính
Do đó: ΔMAB vuông tại M
Suy ra: MA\(\perp\)MB(6)
Từ (5) và (6) suy ra MB//OC

Chọn C.
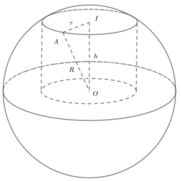
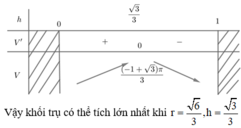
Phương pháp: Dựa vào dữ kiện bài toán lập hàm số và tìm giá trị lớn nhất, nhỏ nhất.


a/ Ta có: xAy = 800 , xAz = 1300 => xAz > xAy => tia Ay nằm giữa tia Az và tia Ax
b/ Có: zAy = xAz - xAy = 130 - 80 = 500
c/ Tự làm =="
O t x y z
a, Trên cùng một nửa mặt phẳng bờ chứa tia Ax có góc xAy < xAz (800<1300) nên tia Ay nằm giữa hai tia Ax và Ay.
b, Vì tia Ay nằm giữa hai tia Ax và Ay nên
xAy+yAz=xAz
800+yAz=1300
yAz=1300-800
yAz=500
Vậy yAz=500
A x t z y
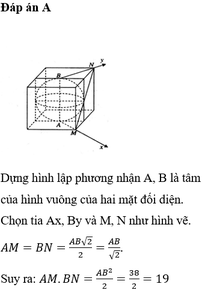

14 nhe ban
14