
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Xét ΔABD và ΔCDB có
AB=CD
\(\widehat{ABD}=\widehat{CDB}\)
BD chung
Do đó: ΔABD=ΔCDB
Suy ra: \(\widehat{IDB}=\widehat{IBD}\)
=>ΔIBD cân tại I
=>IB=ID
Ta có: IA+ID=AD
IB+IC=CB
mà AD=CB
và ID=IB
nên IA=IC
c: Xét ΔOIB và ΔOID có
OI chung
IB=ID
OB=OD
Do đó: ΔOIB=ΔOID
Suy ra: \(\widehat{BOI}=\widehat{DOI}\)
hay OI là tia phân giác của góc xOy

Trước hết ta chứng minh bổ đề sau:
Bổ đề 1: Cho tam giác ABC và 1 điểm M trên cạnh BC. Khi đó: \(\overrightarrow{AM}=\dfrac{MC}{BC}\overrightarrow{AB}+\dfrac{MB}{BC}\overrightarrow{AC}\)
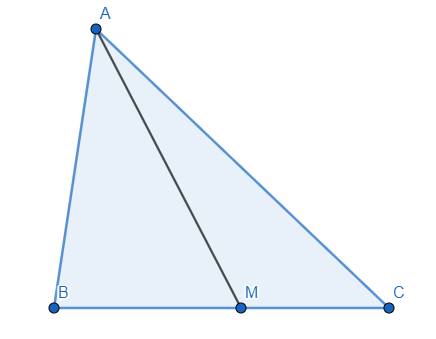
Thật vậy, ta có \(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{BM}{BC}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{BM}{BC}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\left(1-\dfrac{BM}{BC}\overrightarrow{AB}\right)+\dfrac{BM}{BC}\overrightarrow{AC}\)
\(=\dfrac{CM}{BC}\overrightarrow{AB}+\dfrac{BM}{BC}\overrightarrow{AC}\), bổ đề 1 được chứng minh.
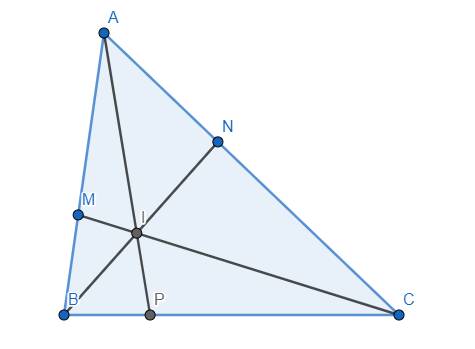
Gọi P là giao điểm của AI và BC. Ta có:
\(\dfrac{MA}{MB}.\dfrac{PB}{PC}.\dfrac{NC}{NA}=1\) \(\Rightarrow x.\dfrac{PB}{PC}.\dfrac{1}{y}=1\) \(\Rightarrow\dfrac{PB}{PC}=\dfrac{y}{x}\) \(\Rightarrow\dfrac{CP}{CB}=\dfrac{x}{x+y}\)
Mặt khác, \(\dfrac{IP}{IA}.\dfrac{MA}{MB}.\dfrac{CB}{CP}=1\) \(\Rightarrow\dfrac{IP}{IA}.x.\dfrac{x+y}{x}=1\) \(\Rightarrow\dfrac{IP}{IA}=\dfrac{1}{x+y}\)
Do đó \(\overrightarrow{AI}=\left(x+y\right)\overrightarrow{IP}\)
Mà theo bổ đề 1: \(\overrightarrow{IP}=\dfrac{PC}{BC}\overrightarrow{IB}+\dfrac{PB}{BC}\overrightarrow{IC}\)
\(=\dfrac{x}{x+y}\overrightarrow{IB}+\dfrac{y}{x+y}\overrightarrow{IC}\)
\(\Rightarrow\overrightarrow{AI}=x\overrightarrow{IB}+y\overrightarrow{IC}\) (đpcm)

a: Xét ΔAIH và ΔMHI có
\(\widehat{AIH}=\widehat{MHI}\)
HI chung
\(\widehat{AHI}=\widehat{MIH}\)
Do đo: ΔAIH=ΔMHI
b: Xét tứ giác AIMH có
MH//AI
MI//AH
Do đó: AIMH là hình bình hành
Suy ra: AI=HM(1)
Xet ΔHMC có \(\widehat{HMC}=\widehat{C}\)
nên ΔHMC cân tại H
=>HM=HC(2)
Từ (1) và (2) suy ra AI=HC

Meeeeeeeeeeeeeeeeeeeeeee!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
có nếu cho mình lấy