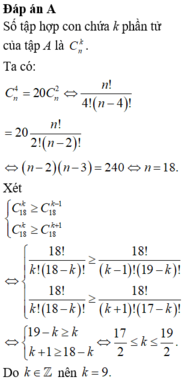Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Mỗi tập con khác rỗng của tập A là một tổ hợp chập k (1 ≤ k ≤ n) của n phần tử của tập A.
Số tập con khác rỗng của tập A gồm k phần tử (1 ≤ k ≤ n) là C n k .
Vậy, số tập con khác rỗng của tập A sẽ là:
![]()
![]()
![]()

Giải thích các bước giải:
Giả sử chúng ta chia được một tập `S=n,n+1,…n+17` của `18` số nguyên dương liên tiếp thành tập `A, B` sao cho ∏n∈Aa=∏n∈Bb và tách của các phần tử trong A bằng tích của các phần tử trong B, nếu 1 tập chứa bội số của 19 thì tập còn lại cũng như thế.
Do vậy, S không chứa bội số nào của 19 hoặc chứa ít nhất hai bội số của 19. Vì có duy nhất 1 trong 18 số nguyên dương liên tiếp có thể là bội của 19, S phải không chứa bội số nào. Bởi vậy `n,n+1,…n+17` lần lượt đồng dư `1,2,3,…,18\ mod\ 19` (chia lấy dư). Do vậy, theo quy tắc Wilson:
∏n∈Aa×∏n∈Bb=n(n+1)+…(n+17)=18!=−1 (mod 19)
Tuy nhiên hai tích của bên trái bằng nhau, điều này không có khả năng vì `-1` không là bình phương của phép mod 19. Bởi vậy, không tồn tại hai tập A và B
Hok tốt!!!!!!!!

Giả sử A = {a, b} với a, b là hai số tự nhiên khác nhau từ 1 đến 15.
Ta có \(\left(1+2+...+15\right)-\left(a+b\right)=ab\)
\(\Leftrightarrow\left(a+1\right)\left(b+1\right)=121\).
Do a, b > 0 nên a = b = 10 (vô lí).
Vậy....

Không gian mẫu: \(A_6^4=360\)
Số biến cố thuận lợi: \(5.4.3.3=180\)
Xác suất: \(P=\dfrac{180}{360}=\dfrac{12}{2}\)

Chọn B
Số tập hợp con của A khác rỗng có số phần tử là số chẵn là:
![]()
Để tính M ta xét: ![]()
![]()
Thay x = 1 ta có: ![]()
![]()
Thay x = -1 ta có: ![]()
![]()
Từ (1) và (2) ta có:

Số cách chọn một quả cầu = tổng số các phần tử của hai tập A, B