Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)CTM: \(R_1nt\left(\left(R_2ntR_3\right)//R_4\right)\)
\(R_{23}=R_2+R_3=7+5=12\Omega\)
\(R_{234}=\dfrac{R_{23}\cdot R_4}{R_{23}+R_4}=\dfrac{12\cdot11}{12+11}=\dfrac{132}{23}\Omega\)
\(R_{tđ}=R_1+R_{234}=3+\dfrac{132}{23}=\dfrac{201}{23}\Omega\)
b)\(I_1=I_{234}=I_{AB}=\dfrac{U_{AB}}{R_{AB}}=\dfrac{30}{\dfrac{201}{23}}=\dfrac{230}{67}A\approx3,4A\)
\(U_{23}=U_4=U-U_1=30-I_1\cdot R_1=30-\dfrac{230}{67}\cdot3=\dfrac{1320}{67}V\)
\(I_4=\dfrac{U_4}{R_4}=\dfrac{\dfrac{1320}{67}}{11}=\dfrac{120}{67}A\approx1,79A\)
\(I_2=I_3=I_{23}=\dfrac{U_{23}}{R_{23}}=\dfrac{\dfrac{1320}{67}}{12}=\dfrac{110}{67}A\approx1,64A\)

Dạng mạch điện [ R1 nt (R2 // R3) ] // R4
a) Điện trở của đoạn mạch ACD là:
\(R_{ACD}=R_1+\dfrac{R_2.R_3}{R_2+R_3}=15+\dfrac{20.20}{20+20}=25\left(\Omega\right)\)
Điện trở tương đương của toàn mạch điện là:
\(R_{tđ}=\dfrac{R_{ACD}.R_4}{R_{ACD}+R_4}=\dfrac{25.10}{25+10}=\dfrac{50}{7}\left(\Omega\right)\)
Vậy.....
b) Vì ampe kế nối tiếp với đèn Đ4 ⇒ \(I_4=I_A=5\left(A\right)\)
Vì R4 // RACB ⇒ UAB = U4 = I4.R4 = 5.10 = 50 (V)
Vì R1 nt RCB ⇒ \(I_1=I_{ACB}=\dfrac{U_{AB}}{R_{ACB}}=\dfrac{50}{25}=2\left(A\right)\)
\(U_{AC}=U_1=I_1.R_1=2.15=30\left(V\right)\)
Vậy....

MCD: R1 nt(R2//R3)
a, ĐIện trở tương đương của đoạn mạch
\(R_{23}=\dfrac{R_2R_3}{R_2+R_3}=\dfrac{30\cdot20}{30+20}=12\left(\Omega\right)\)
\(R_{tđ}=R_1+R_{23}=18+12=30\left(\Omega\right)\)
b,Cường độ dòng điện qua mỗi điện trở
\(I_1=I_{23}=I=\dfrac{U}{R_{tđ}}=\dfrac{60}{30}=2\left(A\right)\)
\(U_2=U_3=U_{23}=I_{23}\cdot R_{23}=2\cdot12=24\left(V\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{24}{30}=0,8\left(A\right)\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{24}{20}=1,2\left(A\right)\)

a,\(R1nt\left(R2//R3\right)=>Rtd=R1+\dfrac{R2R3}{R2+R3}=4+\dfrac{6.3}{6+3}=6\left(om\right)\)
b,\(=>I1=I23=\dfrac{Uab}{Rtd}=\dfrac{9}{6}=1,5A\)
\(=>U23=I23.R23=1,5.\dfrac{6.3}{6+3}=3V=U2=U3\)
\(=>I2=\dfrac{U2}{R2}=\dfrac{3}{6}=0,5A,=>I3=\dfrac{U3}{R3}=\dfrac{3}{3}=1A\)
c,\(=>Im=Ix=I23=\dfrac{1}{3}.1,5=0,5A\)
\(=>RTd=Rx+\dfrac{R2.R3}{R2+R3}=Rx+\dfrac{6.3}{6+3}=\dfrac{U}{Im}=\dfrac{9}{0,5}=18\)
\(=>Rx=16\left(om\right)\)

a)
Ta có sơ đồ mạch điện
( R2//R3)ntR1
Điện trở của đoạn mạch AB là
R23 = 10*15/10+15=6Ω
R123 = Rtđ = 6 + 4 = 10Ω

\(MCD:\left(R1//R2\right)ntR3\)
\(=>R=R12+R3=\dfrac{R1\cdot R2}{R1+R2}+R3=\dfrac{12\cdot6}{12+6}+8=12\Omega\)
\(=>I=I12=I3=\dfrac{U}{R}=\dfrac{24}{12}=2A\)
\(=>U3=I3\cdot R3=2\cdot8=16V\)
\(=>U12=U1=U2=U-U3=24-16=8V\)
\(=>\left\{{}\begin{matrix}I2=U2:R2=8:6=\dfrac{4}{3}A\\I1=U1:R1=8:12=\dfrac{2}{3}A\end{matrix}\right.\)
\(=>A=UIt=24\cdot2\cdot\dfrac{150}{60}=120\)Wh = 0,12kWh
\(=>T=A\cdot1700=0,12\cdot1700=204\left(dong\right)\)

1. a. Theo ht 4' trg đm //, ta có: Rtđ= (R1.R2)/(R1+R2)= (3.6)/(3+6)=2 ôm
b.Theo ĐL ôm, ta có: I= U/Rtđ=24/2=12 A
I1=U/R1=24/3=8 ôm
I2=U/R2=24/6=4 ôm
2. a. Theo ht 4' trg đm //, ta có: Rtđ=(R1.R2.R3)/(R1+R2+R3)= (6.12.4)/(6+12+4)=13,09 ôm
b. Áp dụng ĐL Ôm, ta có: U=I.R=3.13,09=39,27 V
c. Theo ĐL Ôm, ta có:
I1=U/R1=39,27/6=6.545 A
I2=U/R2=39,27/12=3,2725 A
I3=U/R3=39,27/4=9.8175 A
 Trong đó R1=2 ôm, R2=6 ôm, R3=4 ôm, R4=10 ôm. Hiệu điện thế Uab=28v
Trong đó R1=2 ôm, R2=6 ôm, R3=4 ôm, R4=10 ôm. Hiệu điện thế Uab=28v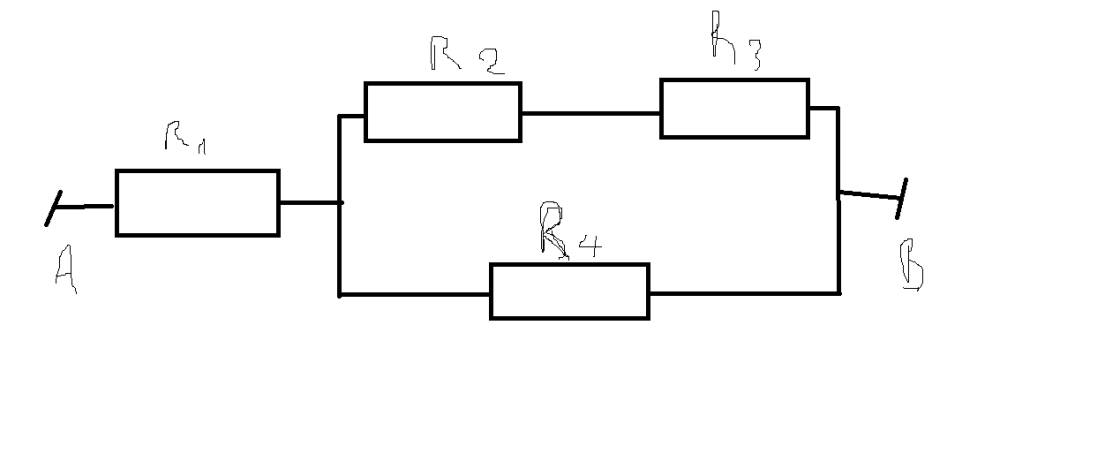
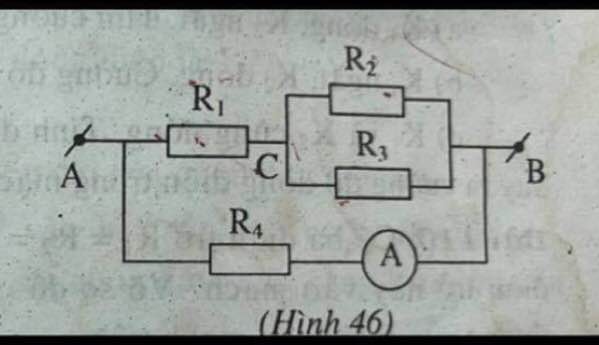
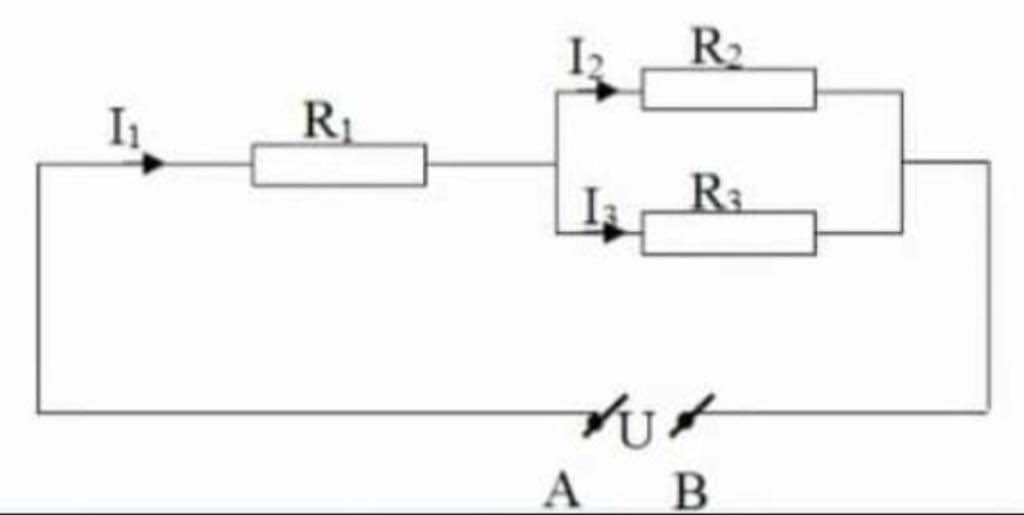

Tóm tắt:
\(R_1=2\Omega\\ R_2=6\Omega\\ R_3=4\Omega\\ R_4=10\Omega\\ U_{AB}=28V\\ a,R_{tđ}=?\\ b,I_1?\\ I_2=?\\ I_3=?\\ I_4=?\\ c,U_1=?\\ U_2=?\)
Giải:
Cấu tạo: R1nt[R4//(R2ntR3)]
\(R_{23}=R_2+R_3=6+4=10\left(\Omega\right)\)
\(R_{234}=\dfrac{R_4\cdot R_{23}}{R_4+R_{23}}=5\Omega\)
\(R_{tđ}=R_1+R_{234}=7\Omega\)
b,\(I_1=I=\dfrac{U_{AB}}{R_{tđ}}=\dfrac{28}{7}=4\left(A\right)\)
\(I_{234}=I_1=4\left(A\right)\)
\(\Rightarrow U_{23}=U_4=U_{234}=I_{234}\cdot R_{234}=4\cdot5=20\left(V\right)\)
\(I_4=\dfrac{U_4}{R_4}=\dfrac{20}{10}=2\left(A\right)\)
\(I_2=I_3=I_{23}=\dfrac{U_{23}}{R_{23}}=\dfrac{20}{10}=2\left(A\right)\)
c,\(U_1=R_1\cdot I_1=2\cdot4=8\left(V\right)\)
\(U_2=I_2\cdot R_2=2\cdot6=12\left(V\right)\)